Question

15．一座桥如图，桥下水面宽度AB是20米，高CD是4米．要使高为3米的船通过，则其宽度须不超过多少米．

（1）如图1，若把桥看做是抛物线的一部分，建立如图坐标系．要使高为3米的船通过，则其宽度须不超过多少米？
（2）如图2，若把桥看做是圆的一部分．要使高为3米的船通过，则其宽度须不超过多少米？

Answer 1

分析 （1）首先利用待定系数法求函数解析式再根据题意得出y=3时，求出x的值即可；
（2）首先构造直角三角形利用BW²=BC²+CW²，再在Rt△WGF中，由题可知，WF=14.5，WG=14.5-1=13.5，根据勾股定理知：GF²=WF²-WG²，求出即可．

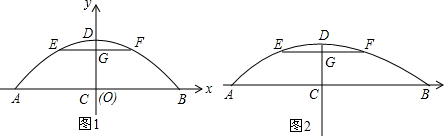
解答 解：（1）设抛物线解析式为：y=ax²+c，
∵桥下水面宽度AB是20米，高CD是4米，
∴A（-10，0），B（10，0），D（0，4），
∴$\left\{\begin{array}{l}{100a+c=0}\\{c=4}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{a=-\frac{1}{25}}\\{c=4}\end{array}\right.$
∴抛物线解析式为：y=-$\frac{1}{25}$x²+4，
∵要使高为3米的船通过，
∴y=3，则3=-$\frac{1}{25}$x²+4，
解得：x=±5，
∴EF=10米；

（2）设圆半径r米，圆心为W，
∵BW²=BC²+CW²，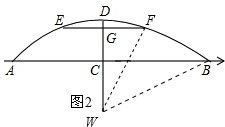
∴r²=（r-4）²+10²，
解得：r=14.5；
在Rt△WGF中，由题可知，WF=14.5，WG=14.5-1=13.5，
根据勾股定理知：GF²=WF²-WG²，
即GF²=14.5²-13.5²=28，
所以GF=2$\sqrt{7}$，
此时宽度EF=4$\sqrt{7}$米．

点评 此题考查了待定系数法求函数解析式以及勾股定理和一元二次方程的应用等知识，利用图象上的点得出解析式是解决问题关键．