
【题目】如图,已知AB是⊙O的直径,点C是⊙O上一点,AD与过点C的切线垂直,垂足为点D,直线DC与AB的延长线相交于点P,弦CE平分∠ACB,交AB于点F,连接BE.
(1)求证:AC平分∠DAB;
(2)求证:△PCF是等腰三角形;
(3)若AF=6,EF=2![]() ,求⊙O的半径长.
,求⊙O的半径长.
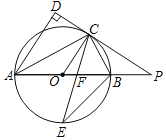
【答案】(1)证明见解析(2)证明见解析(3)4
【解析】
(1)根据切线的性质得OC⊥AD,而AD⊥DP,则肯定判断OC∥AD,根据平行线的性质得∠DAC=∠OCA,加上∠OAC=∠OCA,所以∠OAC=∠DAC;
(2)根据圆周角定理由AB为⊙O的直径得∠ACB=90°,则∠BCE=45°,再利用圆周角定理得∠BOE=2∠BCE=90°,则∠OFE+∠OEF=90°,易得∠CFP+∠OEF=90°,再根据切线的性质得到∠OCF+∠PCF=90°,而∠OCF=∠OEF,根据等角的余角相等得到∠PCF=∠CFP,于是可判断△PCF是等腰三角形;
(3)连结OE.由AB为⊙O的直径,得到∠ACB=90°,根据角平分线的定义得到∠BCE=45°,设⊙O的半径为r,则OF=6-r,根据勾股定理列方程即可得到结论.
(1)证明:∵PD为⊙O的切线,
∴OC⊥DP,
∵AD⊥DP,
∴OC∥AD,
∴∠DAC=∠OCA,
∵OA=OC,
∴∠OAC=∠OCA,
∴∠OAC=∠DAC,
∴AC平分∠DAB;
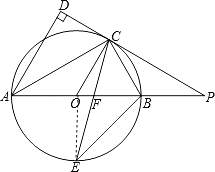
(2)证明:∵AB为⊙O的直径,
∴∠ACB=90°,
∵CE平分∠ACB,
∴∠BCE=45°,
∴∠BOE=2∠BCE=90°,
∴∠OFE+∠OEF=90°,
而∠OFE=∠CFP,
∴∠CFP+∠OEF=90°,
∵OC⊥PD,
∴∠OCP=90°,即∠OCF+∠PCF=90°,
而∠OCF=∠OEF,
∴∠PCF=∠CFP,
∴△PCF是等腰三角形;
(3)解:连结OE.
∵AB为⊙O的直径,∴∠ACB=90°,
∵CE平分∠ACB,∴∠BCE=45°,
∴∠BOE=90°,即OE⊥AB,
设⊙O的半径为r,则OF=6-r,
在Rt△EOF中,∵OE2+OF2=EF2,
∴r2+(6-r)2=(2![]() )2,
)2,
解得,r1=4,r2=2,
当r1=4时,OF=6-r=2(符合题意),
当r2=2时,OF=6-r=4(不合题意,舍去),
∴⊙O的半径r=4.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点A(0,2),B(p,q)在直线上,抛物线m经过点B、C(p+4,q),且它的顶点N在直线l上.
(1)若B(-2,1),
①请在平面直角坐标系中画出直线l与抛物线m的示意图;
②设抛物线m上的点Q的模坐标为e(-2≤e≤0)过点Q作x轴的垂线,与直线l交于点H.若QH=d,当d随e的增大面增大时,求e的取值范围;
(2)抛物线m与y轴交于点F,当抛物线m与x轴有唯一交点时,判断△NOF的形状并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,OA⊥OB,AB⊥x轴于点C,点A(![]() ,1)在反比例函数y=
,1)在反比例函数y=![]() 的图象上.
的图象上.
(1)求反比例函数y=![]() 的表达式;
的表达式;
(2)在x轴上是否存在一点P,使得S△AOP=![]() S△AOB,若存在,求所有符合条件点P的坐标;若不存在,简述你的理由.
S△AOB,若存在,求所有符合条件点P的坐标;若不存在,简述你的理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】合肥周谷堆农副产品批发市场某商铺购进一批红薯,通过商店批发和在淘宝网上进行销售.首月进行了销售情况的统计,其中商店日批发量![]() (百斤)与时间
(百斤)与时间![]() (
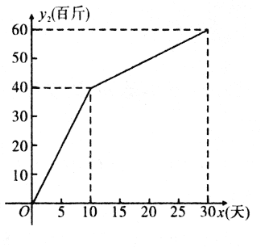
(![]() 为整数,单位:天)的部分对应值如下表所示;在淘宝网上的日销售量
为整数,单位:天)的部分对应值如下表所示;在淘宝网上的日销售量![]() (百斤)与时间
(百斤)与时间![]() (
(![]() 为整数,单位:天)的部分对应值如图所示.
为整数,单位:天)的部分对应值如图所示.
时间 | 0 | 5 | 10 | 150 | 20 | 25 | 30 |
日批发量 | 025 | 40 | 45 | 40 | 25 | 0 |
(1)请你在一次函数、二次函数和反比例函数中,选择合适的函数能反映![]() 与
与![]() 的变化规律,求出
的变化规律,求出![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)设这个月中,日销售总量为![]() ,求出
,求出![]() 与
与![]() 之间的函数关系式,并求出当
之间的函数关系式,并求出当![]() 为何值时,日销售总量
为何值时,日销售总量![]() 最大,最大值为多少?
最大,最大值为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,过B,C两点的⊙O交AC于点D,交AB于点E,连接EO并延长交⊙O于点F.连接BF,CF.若∠EDC=135°,CF=![]() ,则AE2+BE2的值为 ( )
,则AE2+BE2的值为 ( )

A. 8 B. 12 C. 16 D. 20
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小亮玩一个游戏:三张大小、质地都相同的卡片上分别标有数字2,3,4(背面完全相同),现将标有数字的一面朝下.小明从中任意抽取一张,记下数字后放回洗匀,然后小亮从中任意抽取一张,计算小明和小亮抽得的两个数字之和.若和为奇数,则小明胜;若和为偶数,则小亮胜.
(1)请你用画树状图或列表的方法,求出这两数和为6的概率.
(2)你认为这个游戏规则对双方公平吗?说说你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种水果,迸价为每箱40元,规定售价不低于进价.现在的售价为每箱72元,每月可销售60箱.经市场调查发现:若这种牛奶的售价每降低2元,则每月的销量将增加10箱,设每箱水果降价x元(x为偶数),每月的销量为y箱.
(1)写出y与x之间的函数关系式和自变量x的取值范围.
(2)若该超市在销售过程中每月需支出其他费用500元,则如何定价才能使每月销售水果的利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
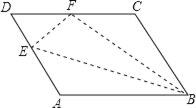
【题目】如图,平行四边形ABCD中,点E在边AD上,以BE为折痕,将△ABE向上翻折,点A正好落在边CD上的点F处,若△DEF的周长为8,△CBF的周长为18,则FC的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
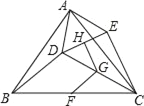
【题目】如图,△ABC为等腰三角形,AB=AC,D为△ABC内一点,连接AD,将线段AD绕点A旋转至AE,使得∠DAE=∠BAC,F,G,H分别为BC,CD,DE的中点,连接BD,CE,GF,GH.
(1)求证:GH=GF;
(2)试说明∠FGH与∠BAC互补.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com