
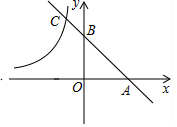
 已知直线y=-x+m与x轴交于点A,与y轴交于点B,反比例函数y=-$\frac{2}{x}$
已知直线y=-x+m与x轴交于点A,与y轴交于点B,反比例函数y=-$\frac{2}{x}$分析 (1)将一次函数解析式代入反比例函数解析式中整理得x2-mx-2=0,由根的判别式△=m2-4×1×(-2)=m2+8>0,即可得出方程有两个不同的实数根,从而证出直线y=-x+m与反比例函数y=-$\frac{2}{x}$的图象总有两个不同的公共点;
(2)过点C作CE⊥x轴于点E,作CF⊥y轴于点F,由直线AC的解析式可得出∠CAE=∠ABF=45°,进而得出AC=$\sqrt{2}$CE、BC=$\sqrt{2}$CF,由点C在反比例函数y=-$\frac{2}{x}$的图象上利用反比例函数系数k的几何意义即可得出CE•CF=|-2|=2,进而可得出AC•BC=2CE•CF=4.
解答 (1)证明:将y=-x+m代入y=-$\frac{2}{x}$,
整理得:x2-mx-2=0,
∵△=m2-4×1×(-2)=m2+8>0,
∴方程有两个不同的实数根,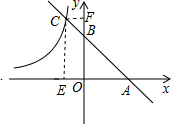
∴直线y=-x+m与反比例函数y=-$\frac{2}{x}$的图象总有两个不同的公共点;
(2)过点C作CE⊥x轴于点E,作CF⊥y轴于点F,如图所示.
∵直线AC的解析式为y=-x+m,
∴∠CAE=∠ABF=45°,
∴AC=$\sqrt{2}$CE,BC=$\sqrt{2}$CF.
∵点C在反比例函数y=-$\frac{2}{x}$的图象上,
∴CE•CF=|-2|=2,
∴AC•BC=$\sqrt{2}$CE•$\sqrt{2}$CF=2CE•CF=4.
点评 本题考查了反比例函数与一次函数的交点问题、根的判别式以及反比例函数图象上点的坐标特征,解题的关键是:(1)将一次函数解析式代入反比例函数解析式中,利用根的判别式找出方程有两个不相等的实数根;(2)根据直线的解析式找出AC=$\sqrt{2}$CE、BC=$\sqrt{2}$CF.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
 如图,过点A的一次函数的图象与正比例函数y=3x的图象相交于点B,则这个一次函数的表达式是( )
如图,过点A的一次函数的图象与正比例函数y=3x的图象相交于点B,则这个一次函数的表达式是( )| A. | y=x+2 | B. | y=2x+5 | C. | y=-x+4 | D. | y=-x+5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 7 | B. | 6 | C. | 5 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
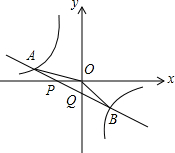 如图,已知直线y=k1x+b与x轴、y轴相交于P、Q两点,与y=$\frac{{k}_{2}}{x}$的图象相交于A(-2,m),B(1,n)两点,连接OA、OB,给出下列结论:①k1+k2>0;②n=-2m;③S△BOQ=-$\frac{1}{2}$b,则正确的是( )
如图,已知直线y=k1x+b与x轴、y轴相交于P、Q两点,与y=$\frac{{k}_{2}}{x}$的图象相交于A(-2,m),B(1,n)两点,连接OA、OB,给出下列结论:①k1+k2>0;②n=-2m;③S△BOQ=-$\frac{1}{2}$b,则正确的是( )| A. | ①② | B. | ②③ | C. | ①③ | D. | ①②③ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
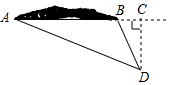 钓鱼岛是我国固有领土,东西长约3641米,如图所示,某海警船巡航到点D处时,测得岛上最东端“东钓角”(A点处)的方向角为北偏西67.5°,最西端“西钓角”(B点处)的方向角为北偏西30°,已知此时海警船到直线AB的距离是2000米,根据以上数据,请求出钓鱼岛东西长度AB的距离,并比较你的计算结果与实际长度的误差(参考数据:tan30°≈0.578,tan67.5°≈2.414,cos30°≈1.732,cot67.5°≈0.414)
钓鱼岛是我国固有领土,东西长约3641米,如图所示,某海警船巡航到点D处时,测得岛上最东端“东钓角”(A点处)的方向角为北偏西67.5°,最西端“西钓角”(B点处)的方向角为北偏西30°,已知此时海警船到直线AB的距离是2000米,根据以上数据,请求出钓鱼岛东西长度AB的距离,并比较你的计算结果与实际长度的误差(参考数据:tan30°≈0.578,tan67.5°≈2.414,cos30°≈1.732,cot67.5°≈0.414)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
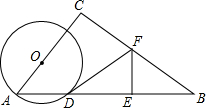 如图,在Rt△ABC中,∠C=90°,tanA=$\frac{4}{3}$,AB=10,点O为AC上一点,以OA为半径作⊙O交AB于点D,BD的中垂线分别交BD,BC于点E,F,连接DF.
如图,在Rt△ABC中,∠C=90°,tanA=$\frac{4}{3}$,AB=10,点O为AC上一点,以OA为半径作⊙O交AB于点D,BD的中垂线分别交BD,BC于点E,F,连接DF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com