
 初中暑期衔接系列答案
初中暑期衔接系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
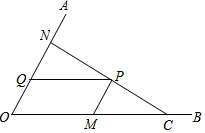 如图,C为∠AOB的边OB上一点,OC=10,N为边OA上异于点O的一动点,P是线段CN上一点,过点P分别作PQ∥OB交OA于点Q,PM∥OA交OB于点M.
如图,C为∠AOB的边OB上一点,OC=10,N为边OA上异于点O的一动点,P是线段CN上一点,过点P分别作PQ∥OB交OA于点Q,PM∥OA交OB于点M.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,某农场要建一个长方形的养兔场,兔场的两边靠墙,两堵墙互相垂直,长度足够长,另两边用木栏围成,木栏总长20m.
如图,某农场要建一个长方形的养兔场,兔场的两边靠墙,两堵墙互相垂直,长度足够长,另两边用木栏围成,木栏总长20m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com