
【题目】如图,在矩形ABCD和矩形PEFG中,AB=8,BC=6,PE=2,PG=4.PE与AC交于点M,EF与AC交于点N,动点P从点A出发沿AB以每秒1个单位长的速度向点B匀速运动,伴随点P的运动,矩形PEFG在射线AB上滑动;动点K从点P出发沿折线PE﹣﹣EF以每秒1个单位长的速度匀速运动.点P、K同时开始运动,当点K到达点F时停止运动,点P也随之停止.设点P、K运动的时间是t秒(t>0). 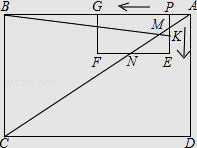
(1)当t=1时,KE= , EN=;
(2)当t为何值时,△APM的面积与△MNE的面积相等?
(3)当点K到达点N时,求出t的值;
【答案】
(1)1;![]()
(2)解:由(1)并结合题意可得,
AP=t,PM= ![]() t,ME=2﹣
t,ME=2﹣ ![]() t,NE=
t,NE= ![]() ﹣t,
﹣t,
∴ ![]() t×
t× ![]() t=
t= ![]() (2﹣
(2﹣ ![]() t)×(
t)×( ![]() ﹣t),
﹣t),
解得,t= ![]() ;
;
(3)解:当点K到达点N时,则PE+NE=AP,
由(2)得, ![]() ﹣t+2=t,
﹣t+2=t,
解得,t= ![]() ;(4)当t为何值时,△PKB是直角三角形?
;(4)当t为何值时,△PKB是直角三角形?
解:①当K在PE边上任意一点时△PKB是直角三角形,
即,0<t≤2;
②当点k在EF上时,
则KE=t﹣2,BP=8﹣t,
∵△BPK∽△PKE,
∴PK2=BP×KE,PK2=PE2+KE2,
∴4+(t﹣2)2=(8﹣t)(t﹣2),
解得t=3,t=4;
③当t=5时,点K在BC边上,∠KBP=90°.
综上,当0<t≤2或t=3或t=4或5时,△PKB是直角三角形.
【解析】解:(1)当t=1时,根据题意得,AP=1,PK=1, ∵PE=2,
∴KE=2﹣1=1,
∵四边形ABCD和PEFG都是矩形,
∴△APM∽△ABC,△APM∽△NEM,
∴ ![]() =
= ![]() ,
, ![]() =
= ![]() ,
,
∴MP= ![]() ,ME=
,ME= ![]() ,
,
∴NE= ![]() ;
;
故答案为:1; ![]() ;
;
(1)利用△APM∽△ABC求出PM,然后求出ME,再利用△APM∽△NEM,就可以求出EN.(2)△APM的面积与△MNE的面积相等,且两个三角形相似,所以,只有两三角形全等面积就相等,表示出三角形的面积,从而求出t值.(3)(1)已经求出EN的值,根据EN+PE=AP的值,解出t即可.(4)是直角三角形有两种情况,K在PE边上任意一点时△PKB是直角三角形,在FE上的一点时也是直角三角形.利用三角形相似求出t的值.


 能考试全能100分系列答案
能考试全能100分系列答案科目:初中数学 来源: 题型:
【题目】已知直线y=kx+b经过点A(0,6),且平行于直线y=-2x.
(1)求该函数的解析式,并画出它的图象;
(2)如果这条直线经过点P(m,2),求m的值;
(3)若O为坐标原点,求直线OP的解析式;
(4)求直线y=kx+b和直线OP与坐标轴所围成的图形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=ax2+bx+3(a≠0)与x轴、y轴分别交于点A(﹣1,0)、B(3,0)、点C三点.
(1)试求抛物线的解析式;
(2)点D(2,m)在第一象限的抛物线上,连接BC、BD.试问,在对称轴左侧的抛物线上是否存在一点P,满足∠PBC=∠DBC?如果存在,请求出点P点的坐标;如果不存在,请说明理由;
(3)如图2,在(2)的条件下,将△BOC沿x轴正方向以每秒1个单位长度的速度向右平移,记平移后的三角形为△B′O′C′.在平移过程中,△B′O′C′与△BCD重叠的面积记为S,设平移的时间为t秒,试求S与t之间的函数关系式?
查看答案和解析>>
科目:初中数学 来源: 题型:
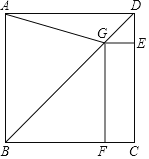
【题目】如图,在正方形ABCD中,点G在对角线BD上![]() 不与点
不与点![]() 重合
重合![]() 于点
于点![]() 于点F,连结AG.
于点F,连结AG.
![]() 写出线段
写出线段![]() 长度之间的数量关系,并说明理由;
长度之间的数量关系,并说明理由;
![]() 若正方形ABCD的边长为
若正方形ABCD的边长为![]() ,求线段BG的长.
,求线段BG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形 ABCD 中,点 G 是边 CD 上一点(不与端点 C,D 重合),以 CG为边在正方形 ABCD 外作正方形 CEFG,且 B、C、E 三点在同一直线上,设正方形 ABCD 和正方形 CEFG 的边长分别为 a 和 b.
(1)分别用含 a,b 的代数式表示图 1 和图 2 中阴影部分的面积 S1、S2;
(2)如果 a+b=5,ab=3,求 S1 的值;
(3)当 S1<S2 时,求![]() 的取值范围.
的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,锐角△ABC中,∠ACB=30°,AB=5,△ABC的面积为23.
(1)若点P在AB边上且CP=![]() ,D,E分别为边AC,BC上的动点.求△PDE周长的最小值;
,D,E分别为边AC,BC上的动点.求△PDE周长的最小值;
(2)假设一只小羊在△ABC区域内,从路边AB某点出发跑到水沟边AC喝水,然后跑向路边BC吃草,再跑回出发点处休息,直接写出小羊所跑的最短路程.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,点E、P在边AB上,且AE=BP,过点E、P作BC的平行线,分别交AC于点F、Q,记△AEF的面积为S1 , 四边形EFQP的面积为S2 , 四边形PQCB的面积为S3 . 
(1)求证:EF+PQ=BC;
(2)若S1+S3=S2 , 求![]() 的值;
的值;
(3)若S3﹣S1=S2 , 直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场投入13 800元资金购进甲、乙两种矿泉水共500箱,矿泉水的成本价和销售价如表所示:
类别/单价 | 成本价 | 销售价(元/箱) |
甲 | 24 | 36 |
乙 | 33 | 48 |
(1)该商场购进甲、乙两种矿泉水各多少箱?
(2)全部售完500箱矿泉水,该商场共获得利润多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com