
【题目】已知抛物线y=x2﹣mx﹣m﹣1与x轴交于A、B两点,点A在点B的左边,与y轴交于点C(0,﹣3).
(1)求点A、B的坐标;
(2)点D是抛物线上一点,且∠ACO+∠BCD=45°,求点D的坐标;
(3)将抛物线向上平移m个单位,交线段BC于点M,N,若∠MON=45°,求m的值.
【答案】(1)点A、B的坐标分别为:(﹣1,0)、(3,0);(2)D(![]() ,﹣
,﹣![]() )或(5,12);(3)m=
)或(5,12);(3)m=![]()
【解析】
(1)把C点的坐标代入解析式可得:﹣m﹣1=﹣3,解得:m=﹣2,即可求解;
(2)①当点D在BC下方时,∠ACO+∠BCD=45°,则AC⊥CD,则直线CD的表达式为:y=![]() x﹣3,联立①②并解得:x=0或
x﹣3,联立①②并解得:x=0或![]() ,即可求解;②当点D(D′)在BC上方时,ED的表达式为:y=﹣x+
,即可求解;②当点D(D′)在BC上方时,ED的表达式为:y=﹣x+![]() ,点H(
,点H(![]() ,﹣
,﹣![]() ),点E的坐标为:(
),点E的坐标为:(![]() ,2),即可求解;
,2),即可求解;
(3)证明△NOM∽△NCO,则NO2=MNCN,即可求解.
(1)把C(0,﹣3)代入解析式可得:﹣m﹣1=﹣3,解得:m=﹣2,
故抛物线的表达式为:y=x2﹣2x﹣3
令y=0,解得:x=3或﹣1,
故点A、B的坐标分别为:(﹣1,0)、(3,0);
(2)①当点D在BC下方时,
∵∠ACO+∠BCD=45°,则AC⊥CD,
设直线AC的解析式为y=k1x-3,代入A(﹣1,0)可得:k1=-3,
∴直线AC的解析式为y=-3x-3,
则直线CD的表达式为:y=![]() x﹣3,
x﹣3,
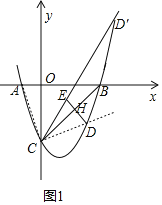
联立得: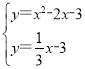 ,解得:x=0或
,解得:x=0或![]() (0舍去),
(0舍去),
故点D(![]() ,﹣
,﹣![]() );
);
②当点D(D′)在BC上方时,
过点D作DE⊥BC交BC于点H,交CD′于点E,则D点、E点关于直线BC对称,
设直线BC的解析式为y=k2x+b,把B(3,0),C(0,-3)代入得:
![]() 解得:
解得:![]()
∴直线BC的表达式为:y=x﹣3
设直线ED的表达式为:y=-x+n,把点D(![]() ,﹣
,﹣![]() )代入得:n=
)代入得:n=![]()
则ED的表达式为:y=﹣x+![]()
联立得: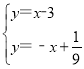 ,解得:x=
,解得:x=![]() ,故点H(
,故点H(![]() ,﹣
,﹣![]() ),根据中点坐标公式可求得点E的坐标为:(
),根据中点坐标公式可求得点E的坐标为:(![]() ,﹣
,﹣![]() ),
),
设直线CE的表达式为y=ax+c,可得 ,解得
,解得![]()
则直线CE的表达式为:y=3x﹣3
联立得: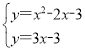 ,解得:x=0或5(0舍去),
,解得:x=0或5(0舍去),
故点D(D′)的坐标为:(5,12),
综上,点D的坐标为:(![]() ,﹣
,﹣![]() )或(5,12);
)或(5,12);
(3)如图2,抛物线平移后的图象为虚线部分,
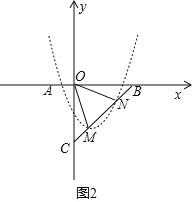
则抛物线的表达式为:y=x2﹣2x﹣3+m(m>0),
则x2﹣2x﹣3+m=x-3,
∴x2﹣3x+m=0,
设点M、N的坐标分别为:(x1,y1)、(x2、y2),
则x1+x2=3,x1x2=m,x2=![]() ,
,
∵∠MON=45°=∠OCM,∠ONM=∠ONM,
∴△NOM∽△NCO,
∴NO2=MNCN,
而NO2=(x22+y2/span>2),MN=![]() (x2﹣x1),CN=
(x2﹣x1),CN=![]() x2,
x2,
即(x22+y22)=2x2(x2﹣x1),
即2x1x2=x22﹣y22,而y2=x2﹣3,
∴2x1x2=6x2﹣9
即2m=![]() ×6﹣9
×6﹣9
解得:m=![]() 或
或![]() (不符合题意,舍去).
(不符合题意,舍去).
∴m=![]()


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,以AC为直径的⊙O交AB于点D,点Q为CA延长线上一点,延长QD交BC于点P,连接OD,∠ADQ=![]() ∠DOQ.
∠DOQ.
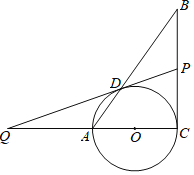
(1)求证:PD是⊙O的切线;
(2)若AQ=AC,AD=4时,求BP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
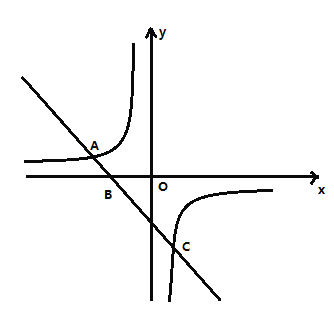
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]()
![]() 的图象交于点
的图象交于点![]() 两点,其中点
两点,其中点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
![]() 求一次函数和反比例函数的表达式;
求一次函数和反比例函数的表达式;
![]() 求
求![]() 点坐标;
点坐标;
![]() 根据图象,直接写出不等式
根据图象,直接写出不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】天水某公交公司将淘汰某一条线路上“冒黑烟”较严重的公交车,计划购买A型和B型两行环保节能公交车共10辆,若购买A型公交车1辆,B型公交车2辆,共需400万元;若购买A型公交车2辆,B型公交车1辆,共需350万元,
(1)求购买A型和B型公交车每辆各需多少万元?
(2)预计在该条线路上A型和B型公交车每辆年均载客量分别为60万人次和100万人次.若该公司购买A型和B型公交车的总费用不超过1220万元,且确保这10辆公交车在该线路的年均载客量总和不少于650万人次,则该公司有哪几种购车方案?哪种购车方案总费用最少?最少总费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
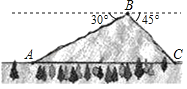
【题目】我市304国道通辽至霍林郭勒段在修建过程中经过一座山峰,如图所示,其中山脚A、C两地海拔高度约为1000米,山顶B处的海拔高度约为1400米,由B处望山脚A处的俯角为30°,由B处望山脚C处的俯角为45°,若在A、C两地间打通一隧道,求隧道最短为多少米(结果取整数,参考数据![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数![]() 的图象经过点
的图象经过点![]() ,直线
,直线![]() 与双曲线交于另一点
与双曲线交于另一点![]() ,作
,作![]() 轴于点
轴于点![]() ,
,![]() 轴于点
轴于点![]() ,连接
,连接![]() .
.
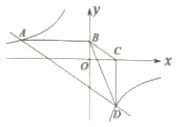
(1)求![]() 的值;
的值;
(2)若![]() ,求直线
,求直线![]() 的解析式;
的解析式;
(3)若![]() ,其它条件不变,直接写出
,其它条件不变,直接写出![]() 与
与![]() 的位置关系.
的位置关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() 为
为![]() 边上的中线,
边上的中线,![]() 于点
于点![]()
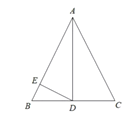
(1)求证:BD·AD=DE·AC.
(2)若AB=13,BC=10,求线段DE的长.
(3)在(2)的条件下,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果商将一种高档水果放在商场销售,该种水果成本价为10元![]() ,售价为40元
,售价为40元![]() ,每天可销售20
,每天可销售20![]() .调查发现,销售单价每下降1元,每天的销售量将增加5
.调查发现,销售单价每下降1元,每天的销售量将增加5![]() .
.
(1)直接写出每天的销售量ykg与降价![]() (元)之间的函数关系式;
(元)之间的函数关系式;
(2)降价多少元时,每天的销售额![]() 元最大,最大是多少元?(销售额=售价×数量)
元最大,最大是多少元?(销售额=售价×数量)
(3)每销售1![]() 水果,需向商场缴纳柜台费
水果,需向商场缴纳柜台费![]() 元(
元(![]() ),水果商计划租赁柜台20天,为了促销,决定开展“每天降价1元”活动,即从第1天开始,每天的销售单价比前一天下降1元(第1天的销售单价为39元),经测算发现,销售的前11天,每天的利润
),水果商计划租赁柜台20天,为了促销,决定开展“每天降价1元”活动,即从第1天开始,每天的销售单价比前一天下降1元(第1天的销售单价为39元),经测算发现,销售的前11天,每天的利润![]() 元随销售天数
元随销售天数![]() (
(![]() 为正整数)的增大而增大,试确定
为正整数)的增大而增大,试确定![]() 的取值范围.(利润=销售额-成本-柜台费)
的取值范围.(利润=销售额-成本-柜台费)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com