
【题目】在△ABC中,∠B=15°,∠C=90°,AB的垂直平分线交AB于点M,交BC于点N.已知BM=12cm,求AC的长. 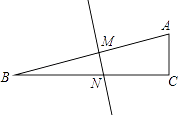
【答案】解:连接NA, ∵MN是线段AB的垂直平分线,
∴MA=MB=12cm,NA=NB,
∴∠MAN=∠B=15°,
∵∠ANC是△ABN的外角,
∴∠ANC=15°+15°=30°,
∴Rt△ACN中,AC= ![]() AN,
AN,
设AC=x,则AN=2x=BN,CN= ![]() x,
x,
∵在Rt△ABC中,AC2+BC2=AB2
∴x2+(2x+ ![]() x)2=242 ,
x)2=242 ,
解得x=12 ![]() ,
,
故AC的长为12 ![]() .
.
【解析】连接NA,由MN是线段AB的垂直平分线可知,NA=NB,∠1=∠B,再根据∠2是△ABN的外角可得出∠2的度数,在Rt△ACN中根据∠2=30°可知AC= ![]() AN,根据勾股定理可得出结论.
AN,根据勾股定理可得出结论.
【考点精析】根据题目的已知条件,利用线段垂直平分线的性质和勾股定理的概念的相关知识可以得到问题的答案,需要掌握垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】甲、乙、丙、丁四人参加训练,近期的10次百米测试平均成绩都是13.2s,方差如下表:
选手 | 甲 | 乙 | 丙 | 丁 |
方差(s2) | 0.020 | 0.019 | 0.021 | 0.022 |
则这四人中发挥最稳定的是( )
A. 甲 B. 乙 C. 丙 D. 丁
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将二次函数y=x2的图象向上平移1个单位,再向右平移2个单位所得图象的解析式是( )
A.y=(x+2)2+1B.y=(x﹣2)2+1C.y=(x﹣2)2﹣1D.y=(x+2)2﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,是真命题的为( )
A.四个角相等的四边形是矩形
B.四边相等的四边形是正方形
C.对角线相等的四边形是菱形
D.对角线互相垂直的四边形是平行四边形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)3+(﹣11)﹣(﹣9)
(2)(﹣7)×5﹣(﹣36)÷4
(3)(1﹣![]() +
+![]() )×(﹣24)
)×(﹣24)
(4)﹣14+![]() ×[2×(﹣6)﹣(﹣4)2].
×[2×(﹣6)﹣(﹣4)2].
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂家生产的一种新型节能灯,为了打开市场出台了相关政策:由厂家协调,厂家按成本价提供产品给经营户自主销售,成本价与出厂价之间的差价由厂家承担.李明按照相关政策投资销售本产品.已知这种节能灯的成本价为每件10元,出厂价为每件12元,每月销售量y(件)与销售单价x(元)之间的关系近似满足一次函数:y=﹣10x+500.
(1)李明在开始销售的第一个月将销售单价定为20元,那么厂家这个月为他承担的总差价为多少元?
(2)设李明获得的利润为w(元),当销售单价定为多少元时,每月可获得最大利润?
(3)物价部门规定,这种节能灯的销售单价不得高于25元.如果李明想要每月获得的利润不低于3000元,那么厂家为他承担的总差价最少为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,∠A=30°,点D是AB的中点,DE⊥BC,垂足为点E,连接CD.
(1)如图1,DE与BC的数量关系是; 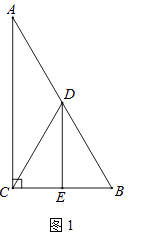
(2)如图2,若P是线段CB上一动点(点P不与点B、C重合),连接DP,将线段DP绕点D逆时针旋转60°,得到线段DF,连接BF,请猜想DE、BF、BP三者之间的数量关系,并证明你的结论; 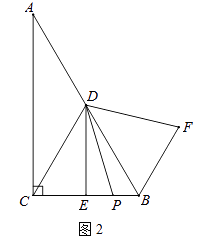
(3)若点P是线段CB延长线上一动点,按照(2)中的作法,请在图3中补全图形,并直接写出DE、BF、BP三者之间的数量关系. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com