
 ��֪��ֱ��y=x+3��x�ᡢy��ֱ��ڵ�A��B��������y=ax2+bx+c��a��b��c����Ϊ0����x�ύ�ڵ�C��D���㣮
��֪��ֱ��y=x+3��x�ᡢy��ֱ��ڵ�A��B��������y=ax2+bx+c��a��b��c����Ϊ0����x�ύ�ڵ�C��D���㣮���� ��1���ټ��������ߵĽ���ʽΪy=a��x-1��2+4����B��0��3������y=a��x-1��2+4�õ�a=-1�����ɽ�����⣮
�������C���꣬��CH��AB��֤����ACH�ǵ���ֱ�������μ��ɽ�����⣮
��2�����ۣ�EF=-a•GE2������G��m��m+3����E��m��$\frac{1}{3}$m+3������ME��AD���Ƴ�M��$\frac{1}{3}$m��$\frac{1}{3}$m+3�����������ߵĽ���ʽΪy=a��x-$\frac{1}{3}$m��2+$\frac{1}{3}m+3$���Ƴ�F��m��-$\frac{4}{9}{m}^{2}$a+$\frac{1}{3}$m+3�����Ƴ�GE=m+3-��$\frac{1}{3}$m+3��=$\frac{2}{3}$m��EF=$\frac{1}{3}$m+3-��-$\frac{4}{9}{m}^{2}$a+$\frac{1}{3}$m+3��=-$\frac{9}{4}$m2a���ɴ˿ɵ�EF=-a•GE2��
��� �⣺��1���١�ֱ��y=x+3��x�ᡢy��ֱ��ڵ�A��B��
��A��-3��0����B��0��3����
�������ߵĶ���MΪ��1��4����
����Լ��������ߵĽ���ʽΪy=a��x-1��2+4��
��B��0��3������y=a��x-1��2+4�õ�a=-1��
�������ߵĽ���ʽΪy=-��x-1��2+4����y=-x2+2x+3��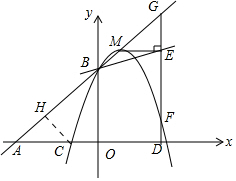
�ڶ���������y=-x2+2x+3����y=0�õ�x=-1��3��
��C��-1��0������CH��AB��H��
��OA=OB����AOB=90�㣬
���OAB=45�㣬
���CAH=��ACH=45�㣬
��AC=2��
��CH=$\sqrt{2}$��
��2�����ۣ�EF=|a|•GE2���������£�
�ٵ�a��0ʱ����ֱ��AB�Ľ���ʽΪy=x+3��ֱ��BE�Ľ���ʽΪy=$\frac{1}{3}$x+3��
����Լ���G��m��m+3����E��m��$\frac{1}{3}$m+3����
��ME��AD��
��M��$\frac{1}{3}$m��$\frac{1}{3}$m+3�����������ߵĽ���ʽΪy=a��x-$\frac{1}{3}$m��2+$\frac{1}{3}m+3$��
��F��m��-$\frac{4}{9}{m}^{2}$a+$\frac{1}{3}$m+3����
��GE=m+3-��$\frac{1}{3}$m+3��=$\frac{2}{3}$m��EF=$\frac{1}{3}$m+3-��-$\frac{4}{9}{m}^{2}$a+$\frac{1}{3}$m+3��=-$\frac{9}{4}$m2a��
��EF=-a•GE2��
��ͬ������a��0ʱ��EF=a•GE2��
����������EF=|a|•GE2��
���� ���⿼����κ����ۺ��⡢һ�κ��������ʡ�����ϵ����������ֱ�������ε����ʵ�֪ʶ������Ĺؼ������������ѧ֪ʶ������⣬ѧ�����ò���������⣬�����п�ѹ���⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ������Ϊ1cm��ֽ����AC�۵���ʹ��ABC=60�㣬���۵����ص����������ε��ܳ�Ϊ��������
��ͼ������Ϊ1cm��ֽ����AC�۵���ʹ��ABC=60�㣬���۵����ص����������ε��ܳ�Ϊ��������| A�� | $\frac{2\sqrt{3}}{3}$ | B�� | 2$\sqrt{3}$ | C�� | $\sqrt{3}$ | D�� | 3$\sqrt{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
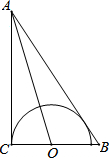 ��ͼ����Rt��ABC�У���ACB=90�㣬��BAC�Ľ�ƽ���߽�BC�ڵ�O��OC=2���Ե�OΪԲ��OCΪ�뾶��Բ��
��ͼ����Rt��ABC�У���ACB=90�㣬��BAC�Ľ�ƽ���߽�BC�ڵ�O��OC=2���Ե�OΪԲ��OCΪ�뾶��Բ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-2��1�� | B�� | ��2��-1�� | C�� | ��1��-2�� | D�� | ��1��2�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
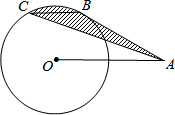 ��ͼ��A�ǰ뾶Ϊ2�ġ�O���һ�㣬OA=4��AB�С�O�ڵ�B����BC��OA������AC����ͼ����Ӱ���ֵ����Ϊ$\frac{2}{3}$�У�
��ͼ��A�ǰ뾶Ϊ2�ġ�O���һ�㣬OA=4��AB�С�O�ڵ�B����BC��OA������AC����ͼ����Ӱ���ֵ����Ϊ$\frac{2}{3}$�У��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
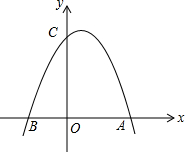 ��ͼ����֪�����߾�����A��3��0����B��-2��0����C��0��6����
��ͼ����֪�����߾�����A��3��0����B��-2��0����C��0��6�����鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com