
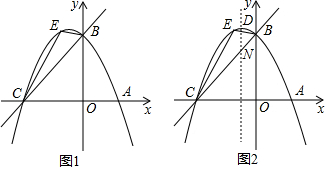
分析 (1)先确定B(0,3),C(4,0),然后利用待定系数法求抛物线解析式;
(2)作EE′∥y轴交BC于E′,如图1,设E(t,-$\frac{3}{8}$t2-$\frac{3}{4}$t+3),则E′(t,$\frac{3}{4}$t+3),则EE′=-$\frac{3}{8}$t2-$\frac{3}{2}$t,所以S△BCE=-$\frac{3}{4}$t2-3t,然后利用二次函数的性质解决问题;
(3)如图2,先利用配方法得到D(-1,$\frac{27}{8}$),再利用一次函数解析式求出N(-1,$\frac{9}{4}$),则DN=$\frac{9}{8}$,设P(m,$\frac{3}{4}$m+3),则F(m,-$\frac{3}{8}$m2-$\frac{3}{4}$m+3),所以PF=-$\frac{3}{8}$m2-$\frac{3}{2}$m,然后根据平行四边形的判定得到-$\frac{3}{8}$m2-$\frac{3}{2}$m=$\frac{9}{8}$,再方程求出m即可得到P点坐标.
解答 解:(1)当x=0时,y=$\frac{3}{4}$x+3=3,则B(0,3),
当y=0时,$\frac{3}{4}$x+3=0,解得x=-4,则(-4,0),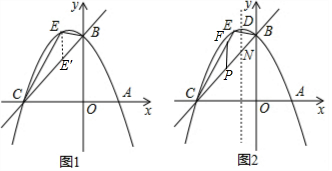
把B(0,3),(-4,0)代入y=ax2-$\frac{3}{4}$x+c得$\left\{\begin{array}{l}{c=3}\\{16a+4+c=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=-\frac{3}{8}}\\{c=3}\end{array}\right.$,
所以抛物线解析式为y=-$\frac{3}{8}$x2-$\frac{3}{4}$x+3;
(2)作EE′∥y轴交BC于E′,如图1,
设E(t,-$\frac{3}{8}$t2-$\frac{3}{4}$t+3),则E′(t,$\frac{3}{4}$t+3),
∴EE′=-$\frac{3}{8}$t2-$\frac{3}{4}$t+3-($\frac{3}{4}$t+3)=-$\frac{3}{8}$t2-$\frac{3}{2}$t,
∴S△BCE=S△ECE′+S△BEE′=$\frac{1}{2}$×4×EE′=-$\frac{3}{4}$t2-3t=-$\frac{3}{4}$(t+2)2+3
当t=-2时,S△BCE有最大值3,此时E点坐标为(-2,3);
(3)存在.
如图2,y=-$\frac{3}{8}$x2-$\frac{3}{4}$x+3=-$\frac{3}{8}$(x+1)2+$\frac{27}{8}$,则D(-1,$\frac{27}{8}$),
当x=-1时,y=$\frac{3}{4}$x+3=$\frac{9}{4}$,则N(-1,$\frac{9}{4}$),
∴DN=$\frac{27}{8}$-$\frac{9}{4}$=$\frac{9}{8}$,
设P(m,$\frac{3}{4}$m+3),则F(m,-$\frac{3}{8}$m2-$\frac{3}{4}$m+3),
则PF=-$\frac{3}{8}$m2-$\frac{3}{4}$m+3-($\frac{3}{4}$m+3)=-$\frac{3}{8}$m2-$\frac{3}{2}$m,
∵PF∥DN,
∴当PF=DN时,四边形DNPF为平行四边形,
即-$\frac{3}{8}$m2-$\frac{3}{2}$m=$\frac{9}{8}$,
整理得m2+4m+3=0,解得m1=-1(舍去),m2=-3,
∴此时P点坐标为(-3,$\frac{3}{4}$).
点评 本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征、二次函数的性质和平行四边形的性质;会利用待定系数法求二次函数的解析式;会求抛物线与坐标轴的交点坐标;理解坐标与图形的关系.


 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案科目:初中数学 来源: 题型:选择题
| 参赛者编号 | 1 | 2 | 3 | 4 | 5 |
| 成绩/分 | 96 | 88 | 86 | 93 | 86 |
| A. | 96,88 | B. | 86,88 | C. | 88,86 | D. | 86,86 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在∠AOB所在的区域内有一个铜矿(用点P表示),点C,D分别表示在边OA,OB上的两个村庄,恰好有CP∥OB,DP∥OA,请在图中利用直尺和圆规确定点P(铜矿)的位置.(要求保留作图痕迹,不写作法)
如图,在∠AOB所在的区域内有一个铜矿(用点P表示),点C,D分别表示在边OA,OB上的两个村庄,恰好有CP∥OB,DP∥OA,请在图中利用直尺和圆规确定点P(铜矿)的位置.(要求保留作图痕迹,不写作法)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 象棋在中国有着三千多年的历史,由于用具简单,趣味性强,成为流行极为广泛的益智游戏.如图,是一局象棋残局,已知表示棋子“馬”和“車”的点的坐标分别为(4,3),(-2,1),则表示棋子“炮”的点的坐标为( )
象棋在中国有着三千多年的历史,由于用具简单,趣味性强,成为流行极为广泛的益智游戏.如图,是一局象棋残局,已知表示棋子“馬”和“車”的点的坐标分别为(4,3),(-2,1),则表示棋子“炮”的点的坐标为( )| A. | (-3,3) | B. | (3,2) | C. | (1,3) | D. | (0,3) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com