
分析 (1)根据有理数的加法,可得答案;
(2)根据有理数的加法,可得答案;
(3)根据单位耗油量乘以行驶路程,可得答案.
解答 解:(1)(+14)+(-13)+(+7)+(-9)+(-8)+(+11)
+(-4)+(-4)+(+13)+(+4)
=14-13+7-9-8+11-4-4+13+4
=+11,
答:距离下午出车时的出发地11千米;
(2)王先生开车行走的路程是:
|+14|+|-13|+|+7|+|-9|+|-8|+|+11|+|-4|+|-4|+|+13|+|4|
=14+13+7+9+8+11+4+4+13+4
=87 千米,
答:共行驶87千米.
(3)耗油:87×0.1=8.7升,
答:这天下午王师傅用了8.7升汽油.
点评 本题考查了正数和负数,利用有理数的加法是解题关键.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
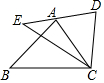 如图所示,△ABC≌△DEC,∠ACB=60°,∠BCD=100°,点A恰好落在线段ED上,则∠B的度数为( )
如图所示,△ABC≌△DEC,∠ACB=60°,∠BCD=100°,点A恰好落在线段ED上,则∠B的度数为( )| A. | 50° | B. | 60° | C. | 55° | D. | 65° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
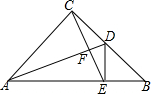 如图所示,△ABC是等腰直角三角形,∠ACB=90°,AD是BC边上的中线,过C作AD的垂线,交AB于点E,交AD于点F.
如图所示,△ABC是等腰直角三角形,∠ACB=90°,AD是BC边上的中线,过C作AD的垂线,交AB于点E,交AD于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 ”表示数据输入、输出框;用“
”表示数据输入、输出框;用“ ”表示数据处理和运算框;用“
”表示数据处理和运算框;用“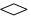 ”表示数据判断框(根据条件决定执行两条路径中的某一条)
”表示数据判断框(根据条件决定执行两条路径中的某一条) ”内,应填×5;第二个运算框“
”内,应填×5;第二个运算框“ ”内,应填-3;
”内,应填-3;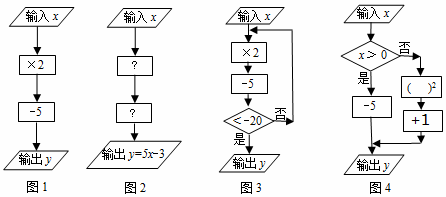
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
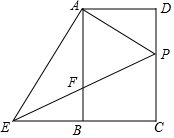 如图,在矩形ABCD中,点P在边DC上,联结AP,过点A作AE⊥AP交CB的延长线于点E,联结EP交边AB于点F.
如图,在矩形ABCD中,点P在边DC上,联结AP,过点A作AE⊥AP交CB的延长线于点E,联结EP交边AB于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com