
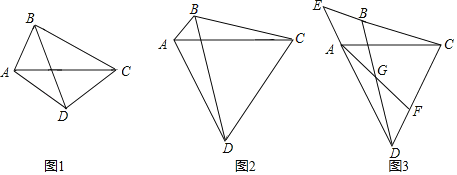
【题目】已知,如图,在△ABC中,AC的垂直平分线与∠ABC的角平分线交于点D,
(1)如图1,判断∠BAD和∠BCD之间的数量关系,并说明理由;
(2)如图2,若∠DAC=60°时,探究线段AB,BC,BD之间的数量关系,并说明理由;
(3)如图3,在(2)的条件下,DA和CB的延长线交于点E,点F是CD上一点且DF=AE,连接AF交BD于点G,若CE=9,求DG的长.
【答案】(1)∠BAD+∠BCD=180°,见解析;(2)BD=AB+BC,见解析;(3)![]() .
.
【解析】
(1)过点D作DG⊥BC于点G,DH⊥BA于点H,根据HL可证明△ADH≌△CDG,可得∠HAD=∠DCG,得出∠BAD+∠BCD=180°;
(2)在BD上截取BF=AB,证明△ABF为等边三角形,△ADC为等边三角形,再证明△ABC≌△AFD,可得出DF=BC,则BD=BF+DF=AB+BC.
(3)延长FD至点M,使DM=DF,证明△EAC≌△MDA,可得AM=CE,∠MAD=∠ECA,可由DG=![]() 得出结果.
得出结果.
(1)∠BAD+∠BCD=180°,理由如下:
如图1,过点D作DG⊥BC于点G,DH⊥BA于点H,
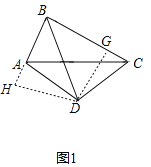
∵AC的垂直平分线与∠ABC角平分线的交于点D,
∴AD=DC,∠ABD=∠DBC,
∴DH=DG,
∴Rt△ADH≌Rt△CDG(HL),
∴∠HAD=∠DCG,
∵∠BAD+∠HAD=180°,
∴∠BAD+∠DCG=180°,
即∠BAD+∠BCD=180°;
(2)BD=AB+BC,理由如下:
如图2,在BD上截取BF=AB,连结AF,
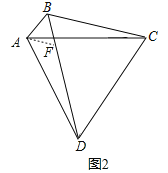
由(1)知∠BAD+∠BCD=180°,
∴∠ABC+∠DAC=180°,
∵∠DAC=60°,
∴∠ABC=120°,
∴∠ABD=∠DBC=60°,
∴△ABF为等边三角形,
∴AB=AF=BF,∠BAF=60°,
∵AD=DC,
∴△ADC为等边三角形,
∴AD=AC,∠DAC=60°,
∴∠DAF=∠BAC,
∴△ABC≌△AFD(SAS),
∴DF=BC,
∴BD=BF+DF=AB+BC.
(3)由(2)知∠DAC=∠DBC=60°,如图3,延长FD至点M,使DM=DF,
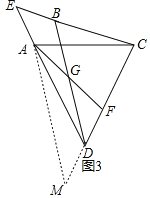
∴∠ACB=∠ADB,
∵DM=DF,DF=AE,
∴DM=AE,
∵∠DAC=∠ADC=60°,
∴∠ADM=∠EAC=120°,
∵AC=AD,
∴△EAC≌△MDA(SAS),
∴AM=CE,∠MAD=∠ECA,
∴∠MAD=∠ADB,
∴DG∥AM,
∵DF=DM,
∴AG=GF,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】解下列方程:
(1)2x(2x+5)=(x﹣1)(2x+5) (2)x2+2x﹣5=0.
(3)x2﹣4x﹣1=0 (用公式法) (4)2x2+1=3x(用配方法)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 为更新果树品种,某果园计划新购进A、B两个品种的果树苗栽植培育,若计划购进这两种果树苗共45棵,其中A种苗的单价为7元/棵,购买B种苗所需费用y(元)与购买数量x(棵)之间存在如图所示的函数关系.
(1)求y与x的函数关系式;
(2)若在购买计划中,B种苗的数量不超过35棵,但不少于A种苗的数量,请设计购买方案,使总费用最低,并求出最低费用.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:
①b<0;②4a+2b+c<0;③a﹣b+c>0;④(a+c)2<b2.其中正确的结论是
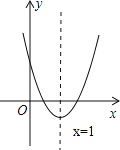
A.①② B.①③ C.①③④ D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,点E,F在边BC上,BE=CF,点D在AF的延长线上,AD=AC.
(1)求证:△ABE≌△ACF;
(2)若∠BAE=30°,则∠ADC= °.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两张等宽的纸条交叉重叠在一起,重叠的部分为四边形ABCD,若测得A,C之间的距离为6cm,点B,D之间的距离为8cm,则线段AB的长为( )
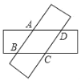
A.5 cmB.4.8 cmC.4.6 cmD.4 cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,BC⊥AB,连结OC,弦AD∥OC,直线CD交BA的延长线于点E.
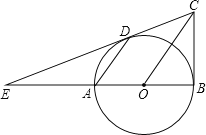
(1)求证:直线CD是⊙O的切线;
(2)若DE=2BC,求AD:OC的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com