
科目:初中数学 来源: 题型:
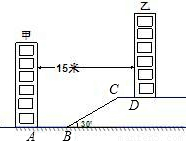
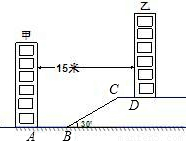
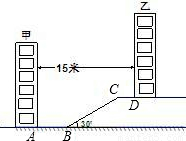
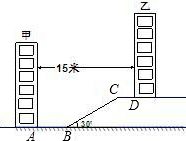 某住宅小区为了美化环境,增加绿地面积,决定在坡地上的甲楼和乙楼之间建一块斜坡草地,如图,已知两楼的水平距离为15米,距离甲楼2米(即AB=2米)开始修建坡角为30°的斜坡,斜坡的顶端距离乙楼4米(即CD=4米),求斜坡BC的长度(结果保留根号).
某住宅小区为了美化环境,增加绿地面积,决定在坡地上的甲楼和乙楼之间建一块斜坡草地,如图,已知两楼的水平距离为15米,距离甲楼2米(即AB=2米)开始修建坡角为30°的斜坡,斜坡的顶端距离乙楼4米(即CD=4米),求斜坡BC的长度(结果保留根号).查看答案和解析>>
科目:初中数学 来源: 题型:
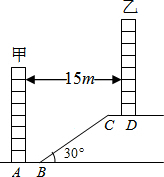 (2010•本溪一模)某住宅小区为了美化环境,增加绿地面积,决定在甲楼和乙楼之间的坡地上建一块斜坡草地为绿化带,如图,已知两楼的水平距离为15米,距离甲楼4米(即AB=4米)开始修建坡角为30°的斜坡,斜坡的顶端距离乙楼2米(即CD=2米),如果绿化带总长为10米,求绿化带的面积.(
(2010•本溪一模)某住宅小区为了美化环境,增加绿地面积,决定在甲楼和乙楼之间的坡地上建一块斜坡草地为绿化带,如图,已知两楼的水平距离为15米,距离甲楼4米(即AB=4米)开始修建坡角为30°的斜坡,斜坡的顶端距离乙楼2米(即CD=2米),如果绿化带总长为10米,求绿化带的面积.(| 3 |
查看答案和解析>>
科目:初中数学 来源:第1章《解直角三角形》中考题集(31):1.5 解直角三角形的应用(解析版) 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2010年云南省楚雄州双柏县中考数学模拟试卷(妥甸中学)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com