
【题目】如图,某水平地面上建筑物的高度为AB,在点D和点F处分别竖立高是2米的标杆CD和EF,两标杆相隔52米,并且建筑物AB,标杆CD和EF在同一竖直平面内,从标杆CD后退2米到点G处,在G处测得建筑物顶端A和标杆顶端C在同一条直线上;从标杆FE后退4米到点H处,在H处测得建筑物顶端A和标杆顶端E在同一条直线上,求建筑物的高.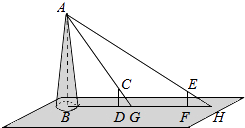
【答案】解:∵AB⊥BH,CD⊥BH,EF⊥BH,
∴AB∥CD∥EF,
∴△CDG∽△ABG,△EFH∽△ABH,
∴ ![]() =
= ![]() ,
, ![]() =
= ![]() ,
,
∵CD=DG=EF=2m,DF=52m,FH=4m,
∴ ![]() =
= ![]() ,
,
![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
解得BD=52,
∴ ![]() =
= ![]() ,
,
解得AB=54.
答:建筑物的高为54米
【解析】首先由AB∥CD∥EF可得出△CDG∽△ABG,△EFH∽△ABH,再根据相似三角形的对应边成比例列出比例式求解即可.
【考点精析】本题主要考查了相似三角形的应用的相关知识点,需要掌握测高:测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决;测距:测量不能到达两点间的举例,常构造相似三角形求解才能正确解答此题.


 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
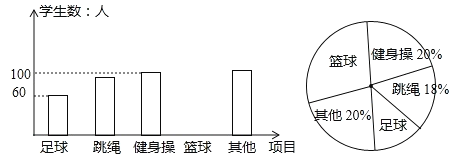
【题目】某市为提高学生参与体育活动的积极性,围绕“你喜欢的体育运动项目(只写一项)”这一问题,对初一新生进行随机抽样调查.下面是根据调查结果绘制成的统计图(不完整).
请你根据图中提供的信息解答下列问题:
(1)本次抽样调查一共调查调查了多少名学生?
(2)根据条形统计图中的数据,求扇形统计图中“最喜欢足球运动”的学生数对应扇形的圆心角度数.
(3)请将条形图补充完整.
(4)若该市2017年约有初一新生21000人,请你估计全市本届学生中“最喜欢足球运动”的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上的三点A、B、C,点A表示的数为5,点B表示的数为-3,点C到点A、点B的距离相等,动点P从点A出发,以每秒2个单位长度的速度沿数轴向左匀速运动,设运动时间为t秒.
(1)点C在数轴上表示的数是______;
(2)当t=______秒时,点P到达点B处:
(3)用含字母t的代数式表示线段AP=______;点P在数轴上表示的数是______.
(4)当P,C之间的距离为1个单位长度时,求t的值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为倡导绿色出行,平阳县在昆阳镇设立了公共自行车服务站点,小明对某站点公共自行车的租用情况进行了调查,将该站点一天中市民每次租用公共自行车的时间t(单位:分)(t≤120)分成A,B,C,D四个组进行各组人次统计,并绘制了如下的统计图,请根据图中信息解答下列问题:
(1)该站点一天中租用公共自行车的总人次为 , 表示A的扇形圆心角的度数是 .
(2)补全条形统计图.
(3)考虑到公共自行车项目是公益服务,公共自行车服务公司规定:市民每次使用公共自行收费2元,已知昆阳镇每天租用公共自行车(时间在2小时以内)的市民平均有5000人次,据此估计公共自行车服务公司每天可收入多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将直角△ABC沿斜边AC的方向平移到△DEF的位置,,ED交BC于点G,BG=4,EF=10,△BEG的面积为4,下列结论:①∠A=∠BED;②△ABC平移的距离是4;③BE=CF;④四边形GCFE的面积为16,正确的有( )

A. ②③B. ①②③C. ①③④D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应党的“文化自信”号召,某校开展了古诗词诵读大赛活动,现随机抽取部分同学的成绩进行统计,并绘制成如下的两个不完整的统计图,请结合图中提供的信息,解答下列问题:
(1)![]() _____,并把频数分布直方图补充完整;
_____,并把频数分布直方图补充完整;
(2)求扇形![]() 的圆心角度数,成绩众数落在多少分之间;
的圆心角度数,成绩众数落在多少分之间;
(3)如果全校有2000名学生参加这次活动,90分以上(含90分)为优秀,那么估计获得优秀奖的学生有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=3,BC=5,点P是BC边上的一个动点(点P不与点B,C重合),现将△PCD沿直线PD折叠,使点C落下点C1处;作∠BPC1的平分线交AB于点E.设BP=x,BE=y,那么y关于x的函数图象大致应为( )
A.
B.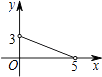
C.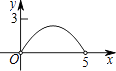
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
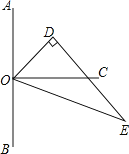
【题目】如图,点O在直线AB上,OC⊥AB,△ODE中,∠ODE=90°,∠EOD=60°,先将△ODE一边OE与OC重合,然后绕点O顺时针方向旋转,当OE与OB重合时停止旋转.
(1)当OD在OA与OC之间,且∠COD=20°时,则∠AOE=______;
(2)试探索:在△ODE旋转过程中,∠AOD与∠COE大小的差是否发生变化?若不变,请求出这个差值;若变化,请说明理由;
(3)在△ODE的旋转过程中,若∠AOE=7∠COD,试求∠AOE的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com