Question

7．将长方形OABC的顶点O与直角坐标系的原点重合，点A，C分别在X轴，Y轴上，点B（a，b），且a，b满足$\sqrt{a-3}$+（b+6）²=0．
（1）求点B的坐标；
（2）若点P从点B出发，以1单位/秒的速度向C点运动（不超过C点），同时点Q从C点出发以2单位/秒的速度向原点运动（不超过原点），试探讨四边形AQCP的面积在运动中是否会发生变化？求其值，若变化，求变化范围．
（3）若过O点的直线OD交长方形的边于点D，且直线OD把长方形的周长分为3：5两部分，求点D的坐标；
（4）若H（0，-1），点P（m，-3）在第三象限内运动，则是否存在点P使四边形HBCP的面积等于△AHB的面积，若存在，求P点坐标，不存在，说明理由．

Answer 1

分析 （1）根据非负数的性质列式求出得到a-3=0，b+6=0，然后解方程求出a与b的值，再写出B点坐标；
（2）设运动的时间为t，则BP=t，CQ=2t（0≤t≤3），则可根据三角形面积公式和S_{四边形AQCP}=S_矩形ABCO-S_△AOQ-S_△APB计算得到S_{四边形AQCP}=9，
即四边形AQCP的面积在运动中不发生变化；
（3）分类讨论：当点D在AB上，如图1，设D（3，n），则AD=-n，BD=6+n，根据题意得（3-n）：（6+n+3+6）=3：5，然后解方程求出n即可得到D点坐标；当点D在BC上，如图2，设D（m，-6），则CD=m，BD=3-m，根据题意得（6+m）：（3-m+3+6）=3：5，然后解方程求出n即可得到D点坐标；
（4）根据四边形HBCP的面积等于△AHB的面积得到$\frac{1}{2}$×5×|m|+$\frac{1}{2}$×5×3=$\frac{1}{2}$×6×3，然后解方程可得到满足条件的m的值，从而得到P点坐标．

解答 解：（1）∵$\sqrt{a-3}$+（b+6）²=0，
∴a-3=0，b+6=0，
∴a=3，b=-6，
∴B点坐标为（3，-6）；
（2）四边形AQCP的面积在运动中不会发生变化．
如图1，设运动的时间为t，则BP=t，CQ=2t（0≤t≤3），
S_{四边形AQCP}=S_矩形ABCO-S_△AOQ-S_△APB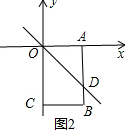
=3×6-$\frac{1}{2}$×3×（6-2t）-$\frac{1}{2}$×6×t
=9；
（3）当点D在AB上，如图3，设D（3，n），则AD=-n，BD=6+n，
∵直线OD把长方形的周长分为3：5两部分，
∴（3-n）：（6+n+3+6）=3：5，
解得n=-$\frac{15}{4}$，
∴D点坐标为（3，-$\frac{15}{4}$）；
当点D在BC上，如图2，设D（m，-6），则CD=m，BD=3-m，
∵直线OD把长方形的周长分为3：5两部分，
∴（6+m）：（3-m+3+6）=3：5，
解得m=$\frac{3}{4}$，
∴D点坐标为（$\frac{3}{4}$，-6），
综上所述，D点坐标为（3，-$\frac{15}{4}$）或（$\frac{3}{4}$，-6）；

（4）存在．如图4，∵四边形HBCP的面积等于△AHB的面积，
∴$\frac{1}{2}$×5×|m|+$\frac{1}{2}$×5×3=$\frac{1}{2}$×6×3，
而m＜0，
∴m=-$\frac{3}{5}$，
∴P点坐标为（-$\frac{3}{5}$，-3）．

点评 本题考查了坐标与图形性质：利用点的坐标特征计算线段的长和判断线段与坐标轴的位置关系．也考查了三角形的面积公式．