
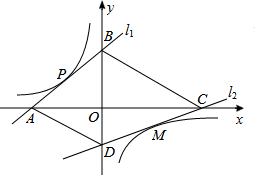
 如图,直线l1解析式为y=x+2,且与坐标轴分别交于A、B两点,与双曲线交于点P(-1,1).点M是双曲线在第四象限上的一点,过点M的直线l2与双曲线只有一个公共点,并与坐标轴分别交于点C、点D,当四边形ABCD的面积取最小值时,则点M的坐标为( )
如图,直线l1解析式为y=x+2,且与坐标轴分别交于A、B两点,与双曲线交于点P(-1,1).点M是双曲线在第四象限上的一点,过点M的直线l2与双曲线只有一个公共点,并与坐标轴分别交于点C、点D,当四边形ABCD的面积取最小值时,则点M的坐标为( )| A. | (1,-1) | B. | (2,-$\frac{1}{2}$) | C. | (3,-$\frac{1}{3}$) | D. | 不能确定 |
分析 先求出A、B两点的坐标,有P(-1,1)在反比例函数图象上求得解析式为y=-$\frac{1}{x}$,设M点横坐标为a,进而可得M点坐标(a,-$\frac{1}{a}$);再设直线l2的解析式为y=bx+c,根据条件“过点M的直线l2与双曲线只有一个公共点”,将M点坐标代入直线l2的解析式,求得用a表示的C、D两点坐标.由A、B、C、D四点坐标,可得AC、BD的长,因为AC⊥BD,有S四边形ABCD=$\frac{1}{2}$AC•BD,据此得到一个关于a的式子,通过化简、配方即可求得S四边形ABCD的最小值,故可得出a的值,由此得出结论.
解答 解:∵直线l1解析式为y=x+2,且与坐标轴分别交于A、B两点,
∴A(-2,0),B(0,2).
设反比例函数的解析式为y=$\frac{k}{x}$,
∵点P(-1,1)在反比例函数y=$\frac{k}{x}$的图象上,
∴k=xy=-1.
∴反比例函数的解析式为y=-$\frac{1}{x}$.
∵点M在第四象限,且在反比例函数y=-$\frac{1}{x}$的图象上,
∴可设点M的坐标为(a,-$\frac{1}{a}$),其中a>0.
设直线l2的解析式为y=bx+c,
则ab+c=-$\frac{1}{a}$.
∴c=-$\frac{1}{a}$-ab.
∴y=bx-$\frac{1}{a}$-ab.
∵直线y=bx-$\frac{1}{a}$-ab与双曲线y=-$\frac{1}{x}$只有一个交点,
∴方程bx-$\frac{1}{a}$-ab=-$\frac{1}{x}$即bx2-($\frac{1}{a}$+ab)x+1=0有两个相等的实根.
∴[-($\frac{1}{a}$+ab)]2-4b=($\frac{1}{a}$+ab)2-4b=($\frac{1}{a}$-ab)2=0.
∴$\frac{1}{a}$=ab.
∴b=$\frac{1}{{a}^{2}}$,c=-$\frac{2}{a}$.
∴直线l2的解析式为y=$\frac{1}{{a}^{2}}$x-$\frac{2}{a}$.
∴当x=0时,y=-$\frac{2}{a}$,则点D的坐标为(0,-$\frac{2}{a}$);
当y=0时,x=2a,则点C的坐标为(2a,0).
∴AC=2a-(-2)=2a+2,BD=2-(-$\frac{2}{a}$)=2+$\frac{2}{a}$.
∵AC⊥BD,
∴S四边形ABCD=$\frac{1}{2}$AC•BD
=$\frac{1}{2}$(2a+2)(2+$\frac{2}{a}$)
=4+2(a+$\frac{1}{a}$)
=4+2[($\sqrt{a}$-$\frac{1}{\sqrt{a}}$)2+2]
=8+2($\sqrt{a}$-$\frac{1}{\sqrt{a}}$)2.
∵($\sqrt{a}$-$\frac{1}{\sqrt{a}}$)2≥0,
∴S四边形ABCD≥8,
∴当且仅当($\sqrt{a}$-$\frac{1}{\sqrt{a}}$)2=0,即a=1时,四边形有最小值,
∴M(1,-1).
故选A.
点评 本题考查的是反比例函数综合题,涉及到用待定系数法求反比例函数及一次函数的解析式、根的判别式、双曲线与直线的交点等知识,考查了用配方法求代数式的最值,突出了对能力的考查,是一道好题.


 名题金卷系列答案
名题金卷系列答案科目:初中数学 来源: 题型:解答题
 -$\frac{{x}^{2}-1}{{x}^{2}-2x+1}$)÷$\frac{x}{x+1}$=$\frac{x+1}{x-1}$
-$\frac{{x}^{2}-1}{{x}^{2}-2x+1}$)÷$\frac{x}{x+1}$=$\frac{x+1}{x-1}$查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①②③ | B. | ①②④ | C. | ②③④ | D. | ①③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
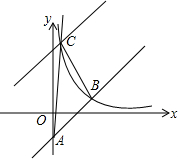 如图,已知直线y=x+a与y轴相交于点A,与反比例函数y=$\frac{k}{x}$(x>0)的图象相交于点B(-a+1,a+4).
如图,已知直线y=x+a与y轴相交于点A,与反比例函数y=$\frac{k}{x}$(x>0)的图象相交于点B(-a+1,a+4).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
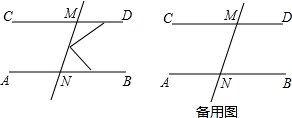 如图1,直线AB∥CD,P是截线MN上的一点.
如图1,直线AB∥CD,P是截线MN上的一点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
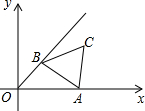 如图,在直角坐标系xOy中,已知正三角形ABC的边长为2,点A从点O开始沿着x轴的正方向移动,点B在∠xOy的平分线上移动.则点C到原点的最大距离是( )
如图,在直角坐标系xOy中,已知正三角形ABC的边长为2,点A从点O开始沿着x轴的正方向移动,点B在∠xOy的平分线上移动.则点C到原点的最大距离是( )| A. | 1+$\sqrt{2}$+$\sqrt{3}$ | B. | $\sqrt{2}$+$\sqrt{6}$ | C. | 2+$\sqrt{3}$ | D. | 1+2$\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com