
【题目】解下列不等式或不等式组,并把它们的解集在数轴上表示出来.
(1)5x+15>4x-13; (2) ![]() ≤
≤![]() ;
;
(3) ![]() (4)
(4) 
【答案】(1)x>-28(2)x![]() -2(3)无解(4)
-2(3)无解(4) ![]() ≤x<3
≤x<3
【解析】试题分析:(1)移项、合并同类项即可;
(2)去分母、移项、合并同类项即可得到结论;
(3)(4)先求出每个不等式的解集,然后求公共解集即可.
试题解析:解:(1)移项,得:5x-4x>-13-15,合并同类项得:x>-28.
不等式的解集在数轴上表示如图.
![]()
(2)去分母,得:2(2x-1)≤3x-4
去括号、移项,得:4x-3x≤2-4
合并同类项得:x≤-2.
不等式的解集在数轴上表示如图.
![]()
(3)解不等式①得:x<-6;
解不等式②得:x>2.
所以原不等式组无解.
不等式组的解集在数轴上表示如图.
![]()
(4)解不等式①得:x≥![]() ;
;
解不等式②得:x<3,
∴原不等式组的解集为![]() ≤x<3.
≤x<3.
不等式组的解集在数轴上表示如图.
![]()


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某公交公司有A,B型两种客车,它们的载客量和租金如下表:
A | B | |
载客量(人/辆) | 45 | 30 |
租金(元/辆) | 400 | 280 |
红星中学根据实际情况,计划租用A,B型客车共5辆,同时送七年级师生到基地参加社会实践活动,设租用A型客车x辆,根据要求回答下列问题:
(1)用含x的式子填写下表:
车辆数(辆) | 载客量(人) | 租金(元) | |
A | x | 45x | 400x |
B | 5-x |
(2)若要保证租车费用不超过1900元,求x的最大值;
(3)在(2)的条件下,若七年级师生共有195人,写出所有可能的租车方案,并确定最省钱的租车方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一个直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿∠CAB的角平分线AD折叠,使它落在斜边AB上,且与AE重合,你能求出CD的长吗?
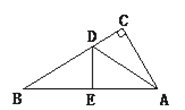
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知,点B,E,C,F在一条直线上,AB=DF,AC=DE,∠A=∠D.
(1)求证:AC∥DE;
(2)若BF=21,EC=9,求BC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A,B,C为一个平行四边形的三个顶点,且A,B,C三点的坐标分别为(3,3),(6,4),(4,6).
(1)请直接写出这个平行四边形第四个顶点的坐标;
(2)求这个平行四边形的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某镇水库的可用水量为12000万m3,假设年降水量不变,能维持该镇16万人20年的用水量.为实施城镇化建设,新迁入了4万人后,水库只能够维持居民15年的用水量.
(1)问:年降水量为多少万m3?每人年平均用水量多少m3?
(2)政府号召节约用水,希望将水库的使用年限提高到25年.则该镇居民人均每年需节约多少m3水才能实现目标?
(3)某企业投入1000万元设备,每天能淡化5000m3海水,淡化率为70%.每淡化1m3海水所需的费用为1.5元,政府补贴0.3元.企业将淡化水以3.2元/m3的价格出售,每年还需各项支出40万元.按每年实际生产300天计算,该企业至少几年后能收回成本(结果精确到个位)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】安宁市的一种绿色蔬菜,若在市场上直接销售,每吨利润为1000元,若经粗加工后销售,每吨利润可达4500元;若经精加工后销售每吨获利7500元.当地一家农产品企业收购这种蔬菜140吨,该企业加工厂的生产能力是:如果对蔬菜进行粗加工,每天可以加工16吨,如果进行精加工,每天可加工6吨,但两种加工方式不能同时进行,受季节条件限制,企业必须在15天的时间将这批蔬菜全部销售或加工完毕,企业研制了四种可行方案:
方案一:全部直接销售;
方案二:全部进行粗加工;
方案三:尽可能多地进行精加工,没有来得及进行精加工的直接销售;
方案四:将一部分进行精加工,其余的进行粗加工,并恰好15天完成.
请通过计算以上四个方案的利润,帮助企业选择一个最佳方案使所获利润最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】附加题:
(1).填空:请用文字语言叙述勾股定理的逆定理:__________.
勾股定理的逆定理所给出的判定一个三角形是直角三角形的方法,和学过的一些其它几何图形的判定方法不同,它通过计算来判断.实际上计算在几何中也是很重要的,从数学方法这个意义上讲,我们学习勾股定理的逆定理,更重要的是拓展思维,进一步体会数学中的各种方法.
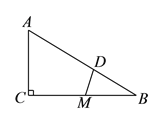
(2).阅读:小明在学习勾股定理后,尝试着利用计算的方法进行论证,解决了如下问题:
如图![]() 中,
中,![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() 于
于![]() ,请说明三条线段
,请说明三条线段![]() 、
、![]() 、
、![]() 总能构成一个直角三角形.
总能构成一个直角三角形.
证明:设![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∵![]() 是
是![]() 的中点,∴
的中点,∴![]() ,
,
在![]() 中,
中,![]() ,
,
在![]() 中,
中,![]() ,
,
消去![]() ,得
,得![]() ,从而,
,从而,![]() ,
,
又因为在![]() 中,
中,![]() ,
,
消去![]() 得
得![]() ,消去
,消去![]() ,所以
,所以![]() ,即
,即![]() .
.
所以,三条线段![]() 、
、![]() 、
、![]() 总能构成一个直角三角形.
总能构成一个直角三角形.
可见,计算在几何证明中也是很重要的.小明正是利用代数中计算、消元等手段,结合相关定理来论证了几何问题.
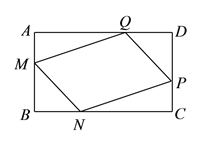
(3).解决问题:在矩形![]() 中,点
中,点![]() 、
、![]() 、
、![]() 、
、![]() 分别在边
分别在边![]() 、
、![]() 、
、![]() 、
、![]() 上,使得
上,使得![]() ,求证:四边形
,求证:四边形![]() 是平行四边形.
是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市公交快速通道开通后,为响应市政府“绿色出行”的号召,家住新城的小王上班由自驾车改为乘坐公交车.已知小王家距上班地点18千米,他用乘公交车的方式平均每小时行驶的路程比他用自驾车的方式平均每小时行驶的路程的2倍还多9千米,他从家出发到达上班地点,乘公交车方式所用时间是自驾车方式所用时间的![]() .小王用自驾车方式上班平均每小时行驶多少千米?
.小王用自驾车方式上班平均每小时行驶多少千米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com