
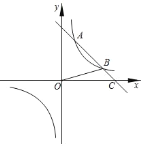
【题目】如图,在平面直角坐标系xOy中,一次函数y=﹣x+4的图象与反比例函数y=![]() (k>0)的图象相交于A,B两点,与x轴相交于点C,连接OB,且
(k>0)的图象相交于A,B两点,与x轴相交于点C,连接OB,且![]() BOC的面积为2.则k=______.
BOC的面积为2.则k=______.
 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:初中数学 来源: 题型:
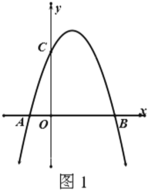
【题目】已知抛物线![]() 与
与![]() 轴交于
轴交于![]() 和
和![]() 两点,与
两点,与![]() 轴正半轴交于
轴正半轴交于![]() 点,若
点,若![]() 的面积
的面积![]() ,
,
(1)求抛物线的对称轴及解析式.
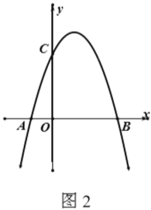
(2)若![]() 为对称轴上一点,且
为对称轴上一点,且![]() ,以
,以![]() 、
、![]() 为顶点作正方形
为顶点作正方形![]() (
(![]() 、
、![]() 、
、![]() 、
、![]() 顺时针排列),若正方形
顺时针排列),若正方形![]() 有两个顶点在抛物线上,求
有两个顶点在抛物线上,求![]() 的值.
的值.
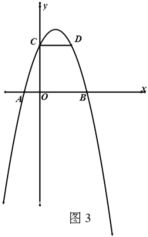
(3)如图,![]() 、
、![]() 两点关于对称轴对称,一次函数
两点关于对称轴对称,一次函数![]() 过
过![]() 点,且与抛物线只有唯一一个公共点,平移直线
点,且与抛物线只有唯一一个公共点,平移直线![]() 交抛物线于
交抛物线于![]() 、
、![]() 两点(
两点(![]() 点在
点在![]() 点上方),请你猜想
点上方),请你猜想![]() 与
与![]() 的数量关系并加以证明.
的数量关系并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知半径为2的⊙O与直线l相切于点A,点P是直径AB左侧半圆上的动点,过点P作直线l的垂线,垂足为C,PC与⊙O交于点D,连接PA、PB,设PC的长为x(2<x<4),则PDCD的最大值是( ).
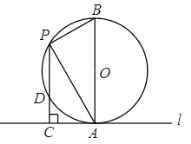
A.2B.3C.4D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
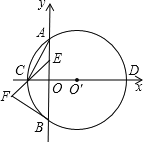
【题目】如下图所示,在直角坐标系中,以![]() 为圆心的
为圆心的![]() 与
与![]() 轴相交于
轴相交于![]() 两点,与
两点,与![]() 轴相交于
轴相交于![]() 两点,连接
两点,连接![]() .
.
(1)![]() 上有一点
上有一点![]() ,使得
,使得![]() .求证
.求证![]() ;
;
(2)在(1)的结论下,延长![]() 到
到![]() 点,连接
点,连接![]() ,若
,若![]() ,请证明
,请证明![]() 与
与![]() 相切;
相切;
(3)如果![]() ,
,![]() 的半径为2,求(2)中直线
的半径为2,求(2)中直线![]() 的解析式.
的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
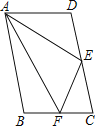
【题目】如图,平行四边形ABCD,点F是BC上的一点,连接AF,∠FAD=60°,AE平分∠FAD,交CD于点E,且点E是CD的中点,连接EF,已知AD=5,CF=3,则EF=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
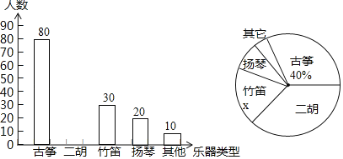
【题目】某校为了了解学生对中国民族乐器的喜爱情况,随机抽取了本校的部分学生进行调查(每名学生选择并且只能选择一种喜爱的乐器),现将收集到的数据绘制成如下两幅不完整的统计图.
(1)这次共抽取 学生调查,扇形统计图中的x= ;
(2)请补全统计图;
(3)在扇形统计图中“扬琴”所对扇形的圆心角是多少度;
(4)若该校有3000名学生,请你估计该校喜爱“二胡”的学生约有多少名.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过直线![]() 上一点
上一点![]() 作
作![]() 轴于点
轴于点![]() ,线段
,线段![]() 交函数
交函数![]() 的图像于点
的图像于点![]() ,点
,点![]() 为线段
为线段![]() 的中点,点
的中点,点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() 的坐标为
的坐标为![]() .
.
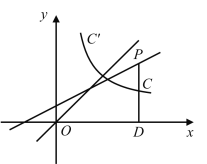
(1)求![]() 、
、![]() 的值;
的值;
(2)求直线![]() 与函数
与函数![]() 图像的交点坐标;
图像的交点坐标;
(3)直接写出不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题呈现
如图1,在边长为1的正方形网格中,连接格点![]() 、
、![]() 和
和![]() 、
、![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,求
,求![]() 的值.
的值.
方法归纳
求一个锐角的三角函数值,我们往往需要找出(或构造出)一个直角三角形.观察发现问题中![]() 不在直角三角形中,我们常常利用网格画平行线等方法解决此类问题.比如连接格点
不在直角三角形中,我们常常利用网格画平行线等方法解决此类问题.比如连接格点![]() 、
、![]() ,可得
,可得![]() ,则
,则![]() ,连接
,连接![]() ,那么
,那么![]() 就变换到中
就变换到中![]() .
.
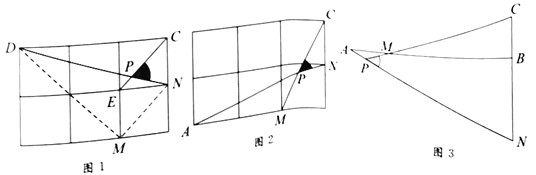
问题解决
(1)直接写出图1中![]() 的值为_________;
的值为_________;
(2)如图2,在边长为1的正方形网格中,![]() 与
与![]() 相交于点
相交于点![]() ,求
,求![]() 的值;
的值;
思维拓展
(3)如图3,![]() ,
,![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() ,延长
,延长![]() 到
到![]() ,使
,使![]() ,连接
,连接![]() 交
交![]() 的延长线于点
的延长线于点![]() ,用上述方法构造网格求
,用上述方法构造网格求![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A的坐标为(0,2),点B的坐标为(1,0),连结AB,以AB为边在第一象限内作正方形ABCD,直线BD交双曲线y═![]() (k≠0)于D、E两点,连结CE,交x轴于点F.
(k≠0)于D、E两点,连结CE,交x轴于点F.

(1)求双曲线y=![]() (k≠0)和直线DE的解析式.
(k≠0)和直线DE的解析式.
(2)求![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com