
【题目】如图,在以点O为原点的直角坐标系中,一次函数y=-![]() x+1的图象与x轴交于A,与y轴交于点B,点C在第二象限内且为直线AB上一点,OC=
x+1的图象与x轴交于A,与y轴交于点B,点C在第二象限内且为直线AB上一点,OC=![]() AB,反比例函数y=
AB,反比例函数y=![]() 的图象经过点C,则k的值为 .
的图象经过点C,则k的值为 .

【答案】-![]() .
.
【解析】
试题解析:如图,在y=-![]() x+1中,令y=0,则x=2;令x=0,得y=1,
x+1中,令y=0,则x=2;令x=0,得y=1,
∴A(2,0),B(0,1).
在Rt△AOB中,由勾股定理得:AB=![]() .
.
设∠BAO=θ,则sinθ=![]() ,cosθ=
,cosθ=![]() .
.
过点O作RT△AOB斜边上的高OE,斜边上的中线OF,则AE=OAcosθ=2×![]() =
=![]() ,OF=
,OF=![]() AB,
AB,
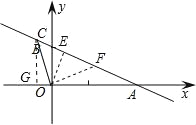
∵OC=![]() AB,
AB,
∴OC=OF=![]() ,
,
∴EF=AE-AF=![]() -
-![]() =
=![]() .
.
∵OC=OF,OE⊥CF,
∴EC=EF=![]() ,
,
∴AC=AE+EC=![]() +
+![]() =
=![]() .
.
过点C作CG⊥x轴于点G,则CG=ACsinθ=![]() ×
×![]() =
=![]() ,
,
AG=ACcosθ=![]() ×
×![]() =
=![]() ,
,
∴OG=AG-OA=![]() -2=
-2=![]() .
.
∴C(-![]() ,
,![]() ).
).
∵反比例函数y=![]() 的图象经过点C,
的图象经过点C,
∴k=-![]() ×
×![]() =-
=-![]() ,
,


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:
【题目】如图,已知点A(1,a)是反比例函数![]() 的图象上一点,直线
的图象上一点,直线![]() 与反比例函数
与反比例函数![]() 的图象在第四象限的交点为点B.
的图象在第四象限的交点为点B.
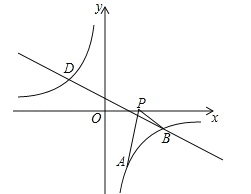
(1)求直线AB的解析式;
(2)动点P(x,0)在x轴的正半轴上运动,当线段PA与线段PB之差达到最大时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
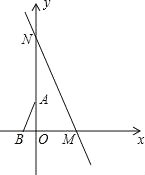
【题目】如图,在直角坐标系中,直线y=-![]() 分别与x轴、y轴交于点M、N,点A、B分别在y轴、x轴上,且∠B=60°,AB=2,将△ABO绕原点O顺时针转动一周,当AB与直线MN平行时点A的坐标为 .
分别与x轴、y轴交于点M、N,点A、B分别在y轴、x轴上,且∠B=60°,AB=2,将△ABO绕原点O顺时针转动一周,当AB与直线MN平行时点A的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列算式:①45;②(-3)20;③0100;④(-1)100;⑤(-1)305;⑥-62.其中,运算结果为正数的有________,运算结果为负数的有________,运算结果为0的有________(填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
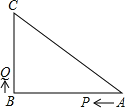
【题目】如图,已知△ABC中,∠B=90°,AB=8cm,BC=6cm,P、Q是△ABC边上的两个动点,其 中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为t秒.
(1)当t=2秒时,求PQ的长;
(2)求出发时间为几秒时,△PQB是等腰三角形?
(3)若Q沿B→C→A方向运动,则当点Q在边CA上运动时,求能使△BCQ成为等腰三角形的运动时间.(直接写答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.
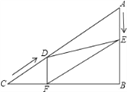
(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值,如果不能,说明理由;
(3)当t为何值时,△DEF为直角三角形?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com