
已知:在菱形ABCD中,O是对角线BD上的一动点.
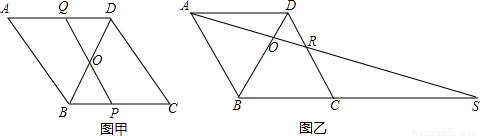
(1)如图,P为线段BC上一点,连接PO并延长交AD于点Q,当O是BD的中点时,求证:OP=OQ;
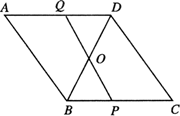
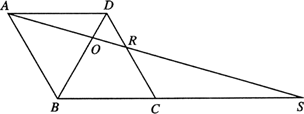
(2)如图,连结AO并延长,与DC交于点R,与BC的延长线交于点S.若AD=4,∠DCB=60°,BS=10,求AS和OR的长.
|
(1)证明:∵ABCD为菱形,∴AD∥BC. ∴∠OBP=∠ODQ ∵O是是 ∴OB=OD 在△BOP和△DOQ中, ∵∠OBP=∠ODQ,OB=OD,∠BOP=∠DOQ ∴△BOP≌△DOQ(ASA) ∴OP=OQ. (2)解:如图,过A作AT⊥BC,与CB的延长线交于T. ∵ABCD是菱形,∠DCB=60° ∴AB=AD=4,∠ABT=60° ∴AT=ABsin60°= TB=ABcos60°=2 ∵BS=10,∴TS=TB+BS=12, ∴AS=
∵AD∥BS,∴△AOD∽△SOB. ∴ 则 ∵AS= 同理可得△ARD∽△SRC. ∴ 则 ∴ ∴OR=OS-RS=. |


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |
查看答案和解析>>
科目:初中数学 来源:2012-2013学年四川省成都七中嘉祥外国语学校九年级(上)月考数学试卷(10月份)(解析版) 题型:解答题
查看答案和解析>>
科目:初中数学 来源:第19章《相似形》中考题集(14):19.6 相似三角形的性质(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com