
ΓΨΧβΡΩΓΩΘ®1Θ©»γΆΦΘ§“―÷ΣΨΊ–Έ![]() ÷–Θ§Βψ
÷–Θ§Βψ![]() «±Ώ
«±Ώ![]() …œΒΡ“ΜΕ·ΒψΘ®≤Μ”κΒψ
…œΒΡ“ΜΕ·ΒψΘ®≤Μ”κΒψ![]() ΓΔ
ΓΔ![]() ÷ΊΚœΘ©Θ§ΙΐΒψ
÷ΊΚœΘ©Θ§ΙΐΒψ![]() Ής
Ής![]() ”ΎΒψ
”ΎΒψ![]() Θ§
Θ§![]() ”ΎΒψ
”ΎΒψ![]() Θ§
Θ§![]() ”ΎΒψ
”ΎΒψ![]() Θ§≤¬œκœΏΕΈ
Θ§≤¬œκœΏΕΈ![]() »ΐ’Ώ÷°ΦδΨΏ”–‘θ―υΒΡ ΐΝΩΙΊœΒΘ§≤Δ÷ΛΟςΡψΒΡ≤¬œκΘΜ
»ΐ’Ώ÷°ΦδΨΏ”–‘θ―υΒΡ ΐΝΩΙΊœΒΘ§≤Δ÷ΛΟςΡψΒΡ≤¬œκΘΜ
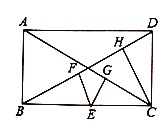
Θ®2Θ©»γΆΦΘ§»τΒψ![]() ‘ΎΨΊ–Έ
‘ΎΨΊ–Έ![]() ΒΡ±Ώ
ΒΡ±Ώ![]() ΒΡ―”≥ΛœΏ…œΘ§ΙΐΒψ
ΒΡ―”≥ΛœΏ…œΘ§ΙΐΒψ![]() Ής
Ής![]() ”ΎΒψ
”ΎΒψ![]() Θ§
Θ§![]() ΫΜ
ΫΜ![]() ΒΡ―”≥ΛœΏ”ΎΒψ
ΒΡ―”≥ΛœΏ”ΎΒψ![]() Θ§
Θ§![]() ”ΎΒψ
”ΎΒψ![]() Θ§‘ρœΏΕΈ
Θ§‘ρœΏΕΈ![]() »ΐ’Ώ÷°ΦδΨΏ”–‘θ―υΒΡ ΐΝΩΙΊœΒΘ§÷±Ϋ”–¥≥ωΡψΒΡΫα¬έΘΜ
»ΐ’Ώ÷°ΦδΨΏ”–‘θ―υΒΡ ΐΝΩΙΊœΒΘ§÷±Ϋ”–¥≥ωΡψΒΡΫα¬έΘΜ
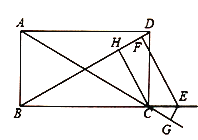
Θ®3Θ©»γΆΦΘ§![]() «’ΐΖΫ–Έ
«’ΐΖΫ–Έ![]() ΒΡΕ‘Ϋ«œΏΘ§
ΒΡΕ‘Ϋ«œΏΘ§![]() ‘Ύ
‘Ύ![]() …œΘ§«“
…œΘ§«“![]() Θ§Ν§Ϋ”
Θ§Ν§Ϋ”![]() Θ§Βψ
Θ§Βψ![]() «
«![]() …œ»Έ“ΜΒψΘ§
…œ»Έ“ΜΒψΘ§![]() ”κΒψ
”κΒψ![]() Θ§
Θ§![]() ”ΎΒψ
”ΎΒψ![]() Θ§≤¬œκœΏΕΈ
Θ§≤¬œκœΏΕΈ![]() ÷°ΦδΨΏ”–‘θ―υΒΡ ΐΝΩΙΊœΒΘ§÷±Ϋ”–¥≥ωΡψΒΡ≤¬œκ.
÷°ΦδΨΏ”–‘θ―υΒΡ ΐΝΩΙΊœΒΘ§÷±Ϋ”–¥≥ωΡψΒΡ≤¬œκ.
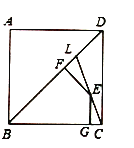
ΓΨ¥πΑΗΓΩΘ®1Θ©![]() Θ§ΦϊΫβΈωΘΜΘ®2Θ©
Θ§ΦϊΫβΈωΘΜΘ®2Θ©![]() Μρ’Ώ
Μρ’Ώ![]() Θ§ΦϊΫβΈωΘΜΘ®3Θ©
Θ§ΦϊΫβΈωΘΜΘ®3Θ©![]() .
.
ΓΨΫβΈωΓΩ
Θ®1Θ©Ιΐ![]() ΒψΉς
ΒψΉς![]() ”Ύ
”Ύ![]() ,œ»ΒΟ≥ωΥΡ±Ώ–Έ
,œ»ΒΟ≥ωΥΡ±Ώ–Έ![]() «ΨΊ–ΈΘ§‘Ό÷ΛΟςΥΡ±Ώ–Έ
«ΨΊ–ΈΘ§‘Ό÷ΛΟςΥΡ±Ώ–Έ![]() «ΨΊ–ΈΘ§÷ΛΟς
«ΨΊ–ΈΘ§÷ΛΟς![]() Θ§«σ≥ω
Θ§«σ≥ω![]() Φ¥Ω…ΘΜ
Φ¥Ω…ΘΜ
Θ®2Θ©ΙΐCΒψΉςCO¥Ι÷±EF,Ω…ΒΟΨΊ–ΈHCOF,“ρΈΣHC=FO,÷Μ“Σ÷ΛΟςEO=EGΘ§ΉνΚσΗυΨίAAS÷ΛΟς![]() .
.
Θ®3Θ©Ν§Ϋ”ACΫΜBD”ΎO,ΙΐΒψEΉςEHΓΆAC,÷ΛΟςΨΊ–ΈFOHE,÷ΛΟςEG=CH,ΗυΨίAAS÷ΛΟς![]() .
.
Θ®1Θ©¥πΘΚ![]()
÷ΛΟςΘΚ»γΆΦ1Θ§Ιΐ![]() ΒψΉς
ΒψΉς![]() ”Ύ
”Ύ![]() Θ°
Θ°
![]() Θ§
Θ§

![]() ΥΡ±Ώ–Έ
ΥΡ±Ώ–Έ![]() «ΨΊ–ΈΘ°
«ΨΊ–ΈΘ°
![]() Θ°
Θ°
![]() Θ°
Θ°
![]() ΥΡ±Ώ–Έ
ΥΡ±Ώ–Έ![]() «ΨΊ–ΈΘ§
«ΨΊ–ΈΘ§
![]() Θ§«“ΜΞœύΤΫΖ÷
Θ§«“ΜΞœύΤΫΖ÷
ΓύΓœDBC=ΓœACB
![]()
![]() Θ§
Θ§
![]() Θ§
Θ§
”÷![]() Θ§
Θ§
![]() Θ°
Θ°
ΓύEG=CN
![]() ΘΜ
ΘΜ
Φ¥![]() ΘΜ
ΘΜ
Θ®2Θ©![]() Μρ’Ώ
Μρ’Ώ![]() ΘΜ
ΘΜ
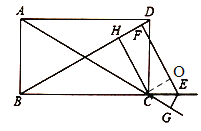
ΙΐCΒψΉςCO¥Ι÷±EF,
ÿ![]() ȧCOâEFȧ
ȧCOâEFȧ![]()
ΓύΨΊ–ΈCOHF
ΓύCEΓΈBDΘ§CH=DO
ΓύΓœDBC=ΓœOCE
ΓΏΨΊ–ΈABCD
ΓύΓœDBC=ΓœACB
ΓΏΓœECG=ΓœACB
ΓύΓœECG=ΓœOCE
ÿCOâEFȧ![]()
ΓύΓœG=ΓœCOE
ΓΏCE=CE
Γύ![]()
ΓύEO=EG
Γύ![]() Μρ’Ώ
Μρ’Ώ![]() ΘΜ
ΘΜ
Θ®3Θ©![]() .
.

Ν§Ϋ”ACΫΜBD”ΎO,ΙΐΒψEΉςEHΓΆAC,
ΓΏ’ΐΖΫ–ΈABCD
ΓύFOΓΆAC,![]()
ΓΏEHΓΆAC
ΓύΨΊ–ΈFEOH,ΓœEHC=90Γψ
ÿEGâBCȧEF=OH
ΓύΓœEGC=90Γψ=ΓœEHC
ΓύEHΓΈBD
ΓύΓœHEC=ΓœFLE
ΓΏBL=BC
ΓύΓœGCE=ΓœFLE
ΓύΓœGCE=ΓœHEC
ΓΏEC=EC
Γύ![]()
ΓύHC=GE
Γύ![]()


 Οϊ–ΘΩΈΧΟœΒΝ–¥πΑΗ
Οϊ–ΘΩΈΧΟœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦ1Θ§Γ―OΒΡ÷±ΨΕAB=12Θ§P «œ“BC…œ“ΜΕ·ΒψΘ®”κΒψBΘ§C≤Μ÷ΊΚœΘ©Θ§ΓœABC=30ΓψΘ§ΙΐΒψPΉςPDΓΆOPΫΜΓ―O”ΎΒψDΘ°
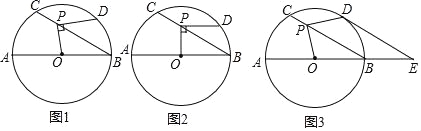
Θ®1Θ©»γΆΦ2Θ§Β±PDΓΈAB ±Θ§«σPDΒΡ≥ΛΘΜ
Θ®2Θ©»γΆΦ3Θ§Β±![]() ±Θ§―”≥ΛAB÷ΝΒψEΘ§ ΙBE=
±Θ§―”≥ΛAB÷ΝΒψEΘ§ ΙBE=![]() ABΘ§Ν§Ϋ”DEΘ°
ABȧͧ۔DEȰ
ΔΌ«σ÷ΛΘΚDE «Γ―OΒΡ«–œΏΘΜ
ΔΎ«σPCΒΡ≥ΛΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
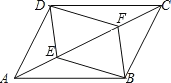
ΓΨΧβΡΩΓΩ“―÷ΣΘΚ»γΆΦΘ§EΓΔF «ΩΎABCDΒΡΕ‘Ϋ«œΏAC…œΒΡΝΫΒψΘ§«“AF=CE.
Δ≈«σ÷ΛΘΚΓςCDFΓ’ΓςABEΘΜ
ΔΤ«σ÷ΛΘΚEDΓΈBF.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΦΉ““ΝΫΗωΙΛ≥ΧΕ”Ζ÷±πΆ§ ±ΩΣΆΎΝΫΧθ600ΟΉ≥ΛΒΡΙήΒάΘ§ΥυΆΎΙήΒά≥ΛΕ»![]() Θ®ΟΉΘ©”κΆΎΨρ ±Φδ
Θ®ΟΉΘ©”κΆΎΨρ ±Φδ![]() Θ®ΧλΘ©÷°ΦδΒΡΙΊœΒ»γΆΦΥυ ΨΘ§‘ρœ¬Ν–ΥΒΖ®÷–ΘΚ
Θ®ΧλΘ©÷°ΦδΒΡΙΊœΒ»γΆΦΥυ ΨΘ§‘ρœ¬Ν–ΥΒΖ®÷–ΘΚ
ΔΌΦΉΕ”ΟΩΧλΆΎ100ΟΉΘΜΔΎ““Ε”ΩΣΆΎΝΫΧλΚσΘ§ΟΩΧλΆΎ50ΟΉΘΜΔέΦΉΕ”±»““Ε”Χα«Α1ΧλΆξ≥…»ΈΈώΘΜΔήΒ±![]() ±Θ§ΦΉ““ΝΫΕ”ΥυΆΎΙήΒά≥ΛΕ»œύΆ§Θ§≤Μ’ΐ»ΖΒΡΗω ΐ”–Θ® Θ©
±Θ§ΦΉ““ΝΫΕ”ΥυΆΎΙήΒά≥ΛΕ»œύΆ§Θ§≤Μ’ΐ»ΖΒΡΗω ΐ”–Θ® Θ©
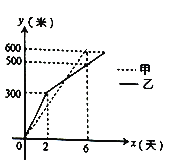
A. 4ΗωB. 3ΗωC. 2ΗωD. 1Ηω
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥ΒΊ÷Ί ”…ζΧ§Ϋ®…ηΘ§¥σΝΠΖΔ’Ι¬Ο”Έ“ΒΘ§ΗςΒΊ¬Ο”ΈΆ≈ΖΉμ≥Εχ÷ΝΘ§Ρ≥¬Ο”ΈΆ≈…œΈγ6 ±¥”¬Ο”ΈΙί≥ωΖΔΘ§≥ΥΤϊ≥ΒΒΫΨύάκ![]() ΒΡ¬Ο”ΈΨΑΒψΙέΙβΘ§ΗΟΤϊ≥Βάκ¬Ο”ΈΙίΒΡΨύάκ
ΒΡ¬Ο”ΈΨΑΒψΙέΙβΘ§ΗΟΤϊ≥Βάκ¬Ο”ΈΙίΒΡΨύάκ![]() ”κ ±Φδ
”κ ±Φδ![]() ΒΡΙΊœΒΩ…“‘”Ο»γΆΦΒΡ’έœΏ±μ Ψ.ΗυΨίΆΦœσΧαΙ©ΒΡ”–ΙΊ–≈œΔΘ§Ϋβ¥πœ¬Ν–Έ ΧβΘΚ
ΒΡΙΊœΒΩ…“‘”Ο»γΆΦΒΡ’έœΏ±μ Ψ.ΗυΨίΆΦœσΧαΙ©ΒΡ”–ΙΊ–≈œΔΘ§Ϋβ¥πœ¬Ν–Έ ΧβΘΚ
Θ®1Θ©«σΗΟΆ≈¬Ο”ΈΨΑΒψ ±ΒΡΤΫΨυΥΌΕ» «Εύ…ΌΘΩ
Θ®2Θ©ΗΟΆ≈‘Ύ¬Ο”ΈΨΑΒψΙέΙβΝΥΕύ…Ό–Γ ±ΘΩ
Θ®3Θ©«σΗΟΆ≈ΖΒΜΊΒΫ±ωΙίΒΡ ±ΩΧ «ΦΗ ±ΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥Βγ ”Χ®ΒΡ“ΜΒΒ”ιά÷–‘ΫΎΡΩ÷–Θ§‘Ύ”ΈœΖPKΜΖΫΎΘ§ΈΣΝΥΥφΜζΖ÷―Γ”ΈœΖΥΪΖΫΒΡΉι‘±Θ§÷ς≥÷»Υ…ηΦΤΝΥ“‘œ¬”ΈœΖΘΚ”Ο≤ΜΆΗΟςΒΡΑΉ≤ΦΑϋΉΓ»ΐΗυ―’…Ϊ≥ΛΕΧœύΆ§ΒΡœΗ…ΰAA1ΓΔBB1ΓΔCC1Θ§÷Μ¬Ε≥ωΥϋΟ«ΒΡΆΖΚΆΈ≤Θ®»γΆΦΥυ ΨΘ©Θ§”…ΦΉΓΔ““ΝΫΈΜΦΈ±ωΖ÷±π¥”ΑΉ≤ΦΝΫΕΥΗς―Γ“ΜΗυœΗ…ΰΘ§≤Δά≠≥ωΘ§»τΝΫ»Υ―Γ÷–Ά§“ΜΗυœΗ…ΰΘ§‘ρΝΫ»ΥΆ§Ε”Θ§Ζώ‘ρΜΞΈΣΖ¥ΖΫΕ”‘±Θ°
Θ®1Θ©»τΦΉΦΈ±ω¥”÷–»Έ“β―Γ‘ώ“ΜΗυœΗ…ΰά≠≥ωΘ§«σΥϊ«ΓΚΟ≥ι≥ωœΗ…ΰAA1ΒΡΗ≈¬ ΘΜ
Θ®2Θ©«κ”ΟΜ≠ ςΉ¥ΆΦΖ®ΜρΝ–±μΖ®Θ§«σΦΉΓΔ““ΝΫΈΜΦΈ±ωΡήΖ÷ΈΣΆ§Ε”ΒΡΗ≈¬ Θ°
![]()
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
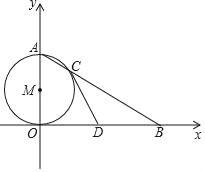
ΓΨΧβΡΩΓΩ»γΆΦΘ§OA «Γ―MΒΡ÷±ΨΕΘ§ΒψB‘Ύx÷α…œΘ§Ν§Ϋ”ABΫΜΓ―M”ΎΒψCΘ°
Θ®1Θ©»τΒψAΒΡΉχ±ξΈΣΘ®0Θ§2Θ©Θ§ΓœABO=30ΓψΘ§«σΒψBΒΡΉχ±ξΘ°
Θ®2Θ©»τDΈΣOBΒΡ÷–ΒψΘ§«σ÷ΛΘΚ÷±œΏCD «Γ―OΒΡ«–œΏΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
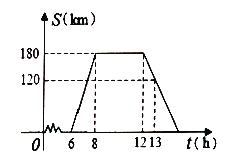
ΓΨΧβΡΩΓΩΫΪ8ΗωΆ§―υ¥σ–ΓΒΡ–Γ’ΐΖΫΧε¥ν≥…»γΆΦΥυ ΨΒΡΦΗΚΈΧεΘ§«κΑ¥’’“Σ«σΫβ¥πœ¬Ν–Έ ΧβΘΚ
Θ®1Θ©¥”’ΐΟφΓΔΉσΟφΓΔ…œΟφΙέ≤λ»γΆΦΥυ ΨΒΡΦΗΚΈΧεΘ§Ζ÷±πΜ≠≥ωΥυΩ¥ΒΫΒΡΦΗΚΈΧεΒΡ–ΈΉ¥ΆΦΘΜ
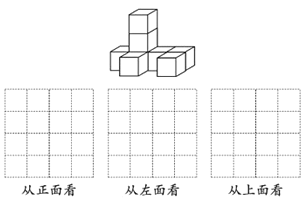
Θ®2Θ©»γΙϊ‘Ύ’βΗωΦΗΚΈΧε…œ‘ΌΑΎΖ≈“ΜΗωœύΆ§ΒΡ–Γ’ΐΖΫΧεΘ§≤Δ±Θ≥÷’βΗωΦΗΚΈΧε¥”…œΟφΩ¥ΚΆ¥”ΉσΟφΩ¥ΒΫΒΡ–ΈΉ¥ΆΦ≤Μ±δ.
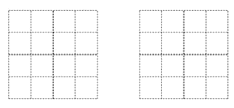
ΔΌΧμΦ”–Γ’ΐΖΫΧεΒΡΖΫΖ®Ι≤”–_________÷÷ΘΜ
ΔΎ«κΜ≠≥ωΝΫ÷÷ΧμΦ”–Γ’ΐΖΫΧεΚσΘ§¥”’ΐΟφΩ¥ΒΫΒΡΦΗΚΈΧεΒΡ–ΈΉ¥ΆΦ.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΗΫΦ”ΧβΘΚΘ®y©¹zΘ©2+Θ®x©¹yΘ©2+Θ®z©¹xΘ©2=Θ®y+z©¹2xΘ©2+Θ®z+x©¹2yΘ©2+Θ®x+y©¹2zΘ©2Θ°
«σ![]() ΒΡ÷ΒΘ°
ΒΡ÷ΒΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΑΌΕ»÷¬–≈ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com