
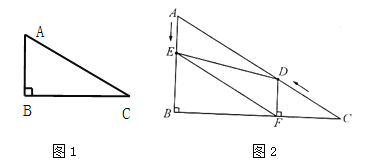
【题目】如图1,在Rt△ABC中,∠B=90°,∠C=30°.
(1)求证:AB=![]() AC;并请你用文字叙述直角三角形的这条性质,把它写在下列横线上:
AC;并请你用文字叙述直角三角形的这条性质,把它写在下列横线上:
;
(2)利用(1)题所得结论继续解答下列问题:
如图2,在Rt△ABC中,∠B=90°,BC=![]() ,∠C=30°.点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连结DE、EF.
,∠C=30°.点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连结DE、EF.
①求证:四边形AEFD是平行四边形;
②当t为何值时,△DEF为直角三角形?请说明理由.
【答案】(1)证明见解析;(2)①证明见解析;②![]() 或4.
或4.
【解析】试题分析:(1)延长AB至P,使BP=AB,连结PC,证明PA=CA ,所以AB= ![]() .
.
(2) ①证明AE,DF平行且相等. ②需分类讨论,当∠EDF=90°时,令△AED是直角三角形,∠ADE=∠C=30°,∴AD=2AE.求t值.当∠EFD=90°时,2AD=AE.求t值.
试题解析:
(1)证明:延长AB至P,使BP=AB,连结PC,
∵ ∠ABC=90°,
∴BC是AP的垂直平分线,
∴AC=CP,
∵∠C=30°,
∴ ∠A=60°,
∴PA=CA,
∴![]() ,
,

这条性质是:在直角三角形中,30°角所对的直角边等于斜边的一半;
(2)①在△DFC中,∠DFC=90°,∠C=30°,DC=2t,∴DF=t,
又∵AE=t,∴AE=DF,
∵AB⊥BC,DF⊥BC,∴AE∥DF
又AE=DF,∴四边形AEFD为平行四边形.
②解得AB=5,AC=10
当∠EDF=90°时,
在Rt△AED中,∠ADE=∠C=30°,∴AD=2AE.即10-2t=2t, ![]() ,
,
当∠DEF=90°时,由(2)知EF∥AD,
∴∠ADE=∠DEF=90°.
∵∠A=90°-∠C=60°,
∴2AD=AE,
即![]()
当∠EFD=90°时,此种情况不存在,
综上所述,当![]() 或4时,△DEF为直角三角形.
或4时,△DEF为直角三角形.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:
【题目】如图,已知A1、A2、……、An、An+1是x轴上的点,且OA1=A1A2=A2A3=……=AnAn+1=1,分别过点A1、A2、……、An、An+1作x轴的垂线交直线y=2x于点B1、B2、……、Bn、Bn+1,连接A1B2、B1A2、A2B3、B2A3、……、AnBn+1、BnAn+1,依次相交于点P1、P2、P3、……、Pn,△A1B1P1、△A2B2P2、……、△AnBnPn的面积依次为S1、S2、……、Sn,则Sn为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若a、b、c为一个三角形的三边长,则式子(a-c)2-b2的值( )
A. 一定为正数 B. 一定为负数
C. 可能是正数,也可能是负数 D. 可能为0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】郑州地铁1号线在2013年12月28日通车之前,为了解市民对地铁票的定价意向,市物价局向社会公开征集定价意见。某学校课外小组也开展了“你认为郑州地铁起步价定为多少合适?”的问卷调查,征求市民的意见,并将某社区市民的问卷调查结果整理后制成了如下统计图:

根据统计图解答:
⑴同学们一共随机调查了 人;
⑵请你把条形统计图补充完整;
⑶假定该社共有1万人,请估计该社区支持“起步价为3元”的市民大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=﹣2x2的图象如何移动,就得到y=﹣2x2+4x+1的图象( )
A.向左移动1个单位,向上移动3个单位
B.向左移动1个单位,向下移动3个单位
C.向右移动1个单位,向上移动3个单位
D.向右移动1个单位,向下移动3个单位
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=2,∠B=∠C=40°.点D在线段BC上运动(点D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E.
(1)当∠BAD=20°时,∠EDC=__________°;
(2)当DC等于多少时,△ABD≌△DCE?试说明理由;
(3)△ADE能成为等腰三角形吗?若能,请直接写出此时∠BAD的度数;若不能,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com