Question

已知：m、n是方程x²-6x+5=0的两个实数根，且m＜n，抛物线y=-x²+bx+c的图象经过点A（m，0）、B（0，n）．
（1）求这个抛物线的解析式；
（2）设（1）中抛物线与x轴的另一交点为C，抛物线的顶点为D，试求出点C、D的坐标和△BCD的面积；
（3）P是线段OC上的一点，过点P作PH⊥x轴，与抛物线交于H点，若直线BC把△PCH分成面积之比为2：3的两部分，请求出P点的坐标．

Answer 1

解：（1）解方程x²-6x+5=0，
得x₁=5，x₂=1
由m＜n，有m=1，n=5
所以点A、B的坐标分别为A（1，0），B（0，5）．
将A（1，0），B（0，5）的坐标分别代入y=-x²+bx+c．
得
解这个方程组，得
所以，抛物线的解析式为y=-x²-4x+5

（2）由y=-x²-4x+5，令y=0，得-x²-4x+5=0
解这个方程，得x₁=-5，x₂=1
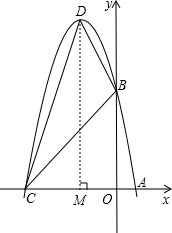
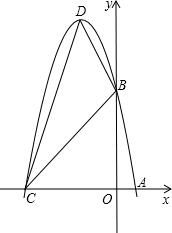
所以C点的坐标为（-5，0）．由顶点坐标公式计算，得点D（-2，9）．
过D作x轴的垂线交x轴于M．
则S_△DMC=×9×（5-2）=
S_梯形MDBO=×2×（9+5）=14，
S_△BOC=×5×5=
所以，S_△BCD=S_梯形MDBO+S_△DMC-S_△BOC=14+-=15．
答：点C、D的坐标和△BCD的面积分别是：（-5，0）、（-2，9）、15；
（3）设P点的坐标为（a，0）
因为线段BC过B、C两点，
所以BC所在的直线方程为y=x+5．
那么，PH与直线BC的交点坐标为E（a，a+5），
PH与抛物线y=-x²-4x+5的交点坐标为H（a，-a²-4a+5）．
由题意，得①EH=EP，
即（-a²-4a+5）-（a+5）=（a+5）
解这个方程，得a=-或a=-5（舍去）
②EH=EP，即（-a²-4a+5）-（a+5）=（a+5）
解这个方程，得a=-或a=-5（舍去），
P点的坐标为（-，0）或（-，0）．
分析：（1）通过解方程即可求出m、n的值，那么A、B两点的坐标就可求出．然后根据A、B两点的坐标即可求出抛物线的解析式．
（2）根据（1）得出的抛物线的解析式即可求出C、D两点的坐标．
由于△BCD的面积无法直接求出，可用其他图形的面积的“和，差关系”来求出．过D作DM⊥x轴于M，那么△BCD的面积=梯形DMOB的面积+△DCM的面积-△BOC的面积．由此可求出△BCD的面积．
（3）由于△PCH被直线BC分成的两个小三角形等高，因此面积比就等于底边的比．如果设PH与BC的交点为E，那么EH就是抛物线与直线BC的函数值的差，而EP就是E点的纵坐标．然后可根据直线BC的解析式设出E点的坐标，然后表示出EH，EP的长．进而可分两种情况进行讨论：①当EH=EP时；②当EH=EP时．由此可得出两个不同的关于E点横坐标的方程即可求出E点的坐标．也就求出了P点的坐标．
点评：命题立意：考查一元二次方程的解法，二次函数解析式的确定、图形的面积求法、函数图象交点等知识及综合应用知识、解决问题的能力．
点评：（1）函数图象交点坐标为两函数解析式组成的方程组的解．
（2）不规则图形的面积通常转化为规则图形的面积的和差．