
【题目】已知,如图 1,六边形 ABCDEF 的每一个内角都相等.
(1)六边形 ABCDEF 每一个内角的度数是 ;
(2)在图 1 中,若 AF 2 ,AB 4 ,BC 3 ,CD 1 ,则 DE ,EF ;
(3)如图 2,在(2)的条件下,若 M 、N 分别为边 AF 、 AB 的中点,连接 CM 、DN交于点 G ,求![]() 的值.
的值.
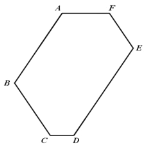
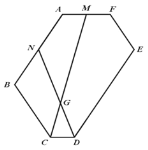
图 1 图 2
【答案】(1) 120°;(2) 5,2 ;(3)![]() .
.
【解析】
(1)用六边形的内角和除以6可得每个内角度数;(2)延长AE,BC,DE,得到一个等边三角形,根据等边三角形性质可求得DE和EF;(3)延长FA、DN交与点P,延长AB、DC交与点Q,证△BQC为等边三角形,求出AN=BN=2,QN=5,QD=4,再证AF∥QD
得![]() ,求出AP,再由AM=1得MP=AP+AM=
,求出AP,再由AM=1得MP=AP+AM=![]() ,所以
,所以![]() .
.
解:(1)120°;
(2)5,2;
(3)延长FA、DN交与点P,延长AB、DC交与点Q,
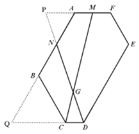
∵∠ABC=∠BCD= 120°,
∴∠QBC=∠QCB= 60°,
∴∠BQC=60°,即△BQC为等边三角形,
∵N为AB的中点,AB=4,
∴AN=BN=2,
∴QN=5,
∵QD=QC+CD,
∴QD=4,
∵∠BAF= 120°,
∴∠BQC+∠BAF= 180°,
∴AF∥QD,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵M为AF的中点,
∴AM=1,
∴MP=AP+AM=![]()
∴![]() ,
,


科目:初中数学 来源: 题型:
【题目】芷江二中为了解学生的体育锻炼情况,随机抽查了部分学生一周参加体育锻炼的时间,得到如图的条形统计图,根据图形解答下列问题:

![]() 这次抽查了多少名学生?
这次抽查了多少名学生?
![]() 所抽查的学生一周平均参加体育锻炼多少小时?
所抽查的学生一周平均参加体育锻炼多少小时?
![]() 已知该校有
已知该校有![]() 名学生,估计该校有多少名学生一周参加体有锻炼的时间超过
名学生,估计该校有多少名学生一周参加体有锻炼的时间超过![]() 小时?
小时?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个口袋中有4个完全相同的小球,把它们分别标号为![]() .
.
![]() 随机摸取一个小球,求恰好摸到标号为2的小球的概率;
随机摸取一个小球,求恰好摸到标号为2的小球的概率;
![]() 随机摸取一个小球然后放回,再随机摸取一个小球,请用列表法或树形图画出所有的可能性,并求两次摸取的小球的标号的和为5的概率.
随机摸取一个小球然后放回,再随机摸取一个小球,请用列表法或树形图画出所有的可能性,并求两次摸取的小球的标号的和为5的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若 二 次 函 数 y ax bx c 的 图 象 与 x 轴 交 于 A 和 B 两 点 , 顶 点 为 C , 且b 4ac 4 ,则 ACB 的度数为()
A. 120° B. 90° C. 60° D. 30°
查看答案和解析>>
科目:初中数学 来源: 题型:
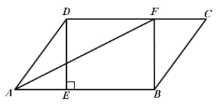
【题目】如图,在平行四边形 ABCD 中,过点 D 作 DE AB 于点 E ,点 F在边 CD 上, DF BE ,连接 AF , BF .
(1)求证:四边形 BFDE 是矩形;
(2)若 AF 平分 DAB , CF3,BF4 ,求 DF 长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,在 ABC 中, ACB 90, B 60, BC 2 ,MON 30.
(1)如图 1, MON 的边 MO ⊥ AB ,边 ON 过点 C ,求 AO 的长;
(2)如图 2,将图 1 中的 MON 向右平移,MON 的两边分别与 ABC 的边 AC 、BC
相交于点 E 、 F ,连接 EF ,若 OEF 是直角三角形,求 AO 的长;
(3)在(2)的条件下,MON 与 ABC 重叠部分面积是否存在最大值,若存在,求出 最大值,若不存在,请说明理由.
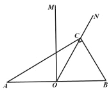
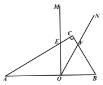
图 1 图 2 备用图
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高.得到下面四个结论:①OA=OD;②AD⊥EF;③当∠A=90°时,四边形AEDF是正方形;④![]() .上述结论中正确的是( )
.上述结论中正确的是( )
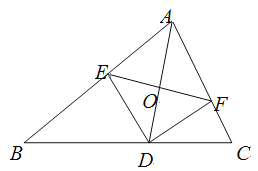
A. ②③ B. ②④ C. ①②③ D. ②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com