Question

9．一张半径为R的半圆图纸沿它的一条弦折叠，使其弧与直径相切，如图所示，O为半圆圆心，如果切点分直径之比为3：2，则折痕长为$\frac{\sqrt{74}}{5}$R．

Answer 1

分析 如图，作O点关于AB的对称点O′，则点O′为弧ADB所在圆的圆心，连结O′D，则O′D⊥EF，O′D=R，先利用ED：DF=3：2计算出DF=$\frac{2}{5}$•2R=$\frac{4}{5}$R，则OD=$\frac{1}{5}$R，再在Rt△O′OD中利用勾股定理计算出O′=$\frac{\sqrt{26}}{5}$R，则OC=$\frac{1}{2}$O′O=$\frac{\sqrt{26}}{10}$R，然后在Rt△AOC中根据勾股定理可计算出AC=$\frac{\sqrt{74}}{10}$R，再利用垂径定理可得AB=2AC=$\frac{\sqrt{74}}{5}$R．

解答 解：如图，作O点关于AB的对称点O′，则点O′为弧ADB所在圆的圆心，
连结O′D，则O′D⊥EF，O′D=R，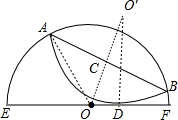
∵ED：DF=3：2，
∴DF=$\frac{2}{5}$•2R=$\frac{4}{5}$R，
∴OD=$\frac{1}{5}$R，
在Rt△O′OD中，OO′=$\sqrt{（\frac{1}{5}R）^{2}+{R}^{2}}$=$\frac{\sqrt{26}}{5}$R，
∴OC=$\frac{1}{2}$O′O=$\frac{\sqrt{26}}{10}$R，
在Rt△AOC，AC=$\sqrt{{R}^{2}-（\frac{\sqrt{26}R}{10}）^{2}}$=$\frac{\sqrt{74}}{10}$R，
∵OC⊥AB，
∴AC=BC，
∴AB=2AC=$\frac{\sqrt{74}}{5}$R．
即折痕长为$\frac{\sqrt{74}}{5}$R．
故答案为$\frac{\sqrt{74}}{5}$R．

点评 本题考查了切线的性质：圆的切线垂直于经过切点的半径．运用切线的性质来进行计算或论证，常通过作辅助线连接圆心和切点，利用垂直构造直角三角形解决有关问题．也考查了垂径定理．