
【题目】如图1、2是底面半径为1cm,母线长为2cm的圆柱体和圆锥体模型.现要用长为2πcm,宽为4cm的长方形彩纸(如图3)装饰圆柱、圆锥模型表面.已知一个圆柱和一个圆锥模型为一套,长方形彩纸共有122张,用这些纸最多能装饰多少套模型呢? 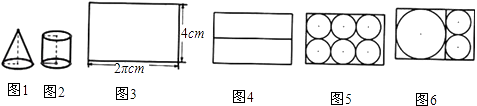 老师:“长方形纸可以怎么裁剪呢?”
老师:“长方形纸可以怎么裁剪呢?”
学生甲:“可按图4方式裁剪出2张长方形.”
学生乙:“可按图5方式裁剪出6个小圆.”
学生丙:“可按图6方式裁剪出1个大圆和2个小圆.”
老师:尽管还有其他裁剪方法,但为裁剪方便,我们就仅用这三位同学的裁剪方法!
(1)计算:圆柱的侧面积是cm2 , 圆锥的侧面积是cm2 .
(2)1张长方形彩纸剪拼后最多能装饰个圆锥模型;5张长方形彩纸剪拼后最多能装饰个圆柱体模型.
(3)求用122张彩纸对多能装饰的圆锥、圆柱模型套数.
【答案】
(1)4π;2π
(2)2;6
(3)解:设做x套模型,则每套模型中做圆锥的需要 ![]() 张纸,作圆柱需要
张纸,作圆柱需要 ![]() 张纸,
张纸,
∴ ![]() +
+ ![]() ≤122,
≤122,
解得:x≤ ![]() ,
,
∵x是6的倍数,取x=90,做90套模型后剩余长方形纸片的张数是
122﹣(45+75)=2张,
2张纸够用这三位同学的裁剪方法不能做一套模型.
∴最多能做90套模型.
【解析】解:(1)圆柱的地面底面周长是2π,则圆柱的侧面积是2π×2=4πcm2 , 圆锥的侧面积是 ![]() ×2π×2=2πcm2;(2)圆柱的底面积是:πcm2 , 则圆柱的表面积是:6πcm2 , 圆锥的表面积是:3πcm2 . 一张纸的面积是:4×2π=8π,
×2π×2=2πcm2;(2)圆柱的底面积是:πcm2 , 则圆柱的表面积是:6πcm2 , 圆锥的表面积是:3πcm2 . 一张纸的面积是:4×2π=8π,
则1张长方形彩纸剪拼后最多能装饰 2个圆锥模型;5张长方形彩纸剪拼后最多能装饰6个圆柱体模型,
【考点精析】关于本题考查的圆锥的相关计算和圆柱的相关计算,需要了解圆锥侧面展开图是一个扇形,这个扇形的半径称为圆锥的母线;圆锥侧面积S=πrl;V圆锥=1/3πR2h.;圆柱的体积: V圆柱=πR2h才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,点E在边AD上,联结CE并延长,交对角线BD于点F,交BA的延长线于点G,如果DE=2AE,那么CF:EF:EG= . 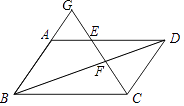
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某教师就中学生对课外数阅读状况进行了一次问卷调查,并根据调查结果绘制了中学生每学期阅读课外书籍数量的统计图(不完整).设x表示阅读书籍的数量(x为正整数,单位:本),其中A:1≤x≤2;B:3≤x≤4;C:5≤x≤6;D:x≥7.请你根据两幅图提供的信息解答下列问题: 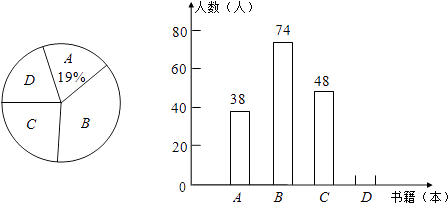
(1)本次共调查了多少名学生?
(2)补全条形统计图,并判断中位数在哪一组;
(3)计算扇形统计图中扇形D的圆心角的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合探究:如图1,在平面直角坐标系xOy中,抛物线y=﹣ ![]() 与x轴交于点A(﹣6,0)和点B(点A在点B左侧),与y轴交于点C,点P为线段AO上的一个动点,过点P作x轴的垂线l与抛物线交于点E,连接AE,EC.
与x轴交于点A(﹣6,0)和点B(点A在点B左侧),与y轴交于点C,点P为线段AO上的一个动点,过点P作x轴的垂线l与抛物线交于点E,连接AE,EC.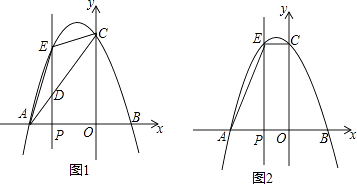
(1)求抛物线的表达式及点C的坐标;
(2)连接AC交直线l于点D,则在点P运动过程中,当点D为EP中点时,S△ADP:S△CDE=;
(3)如图2,当EC∥x轴时,点P停止运动,此时,在抛物线上是否存在点G,使得以点A,E,G为顶点的三角形是直角三角形?若存在,请求出点G的坐标,若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知购买1个足球和1个篮球共需130元,购买2个足球和3个篮球共需340元.
(1)求每个足球和每个篮球的售价;
(2)如果某校计划购买这两种球共54个,总费用不超过4000元,问最多可买多少个篮球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△COD是△AOB绕点O顺时针方向旋转30°后所得的图形,点C恰好在AB上,∠AOD=90°. 
(1)∠B的度数是;
(2)若AO= ![]() ,CD与OB交于点E,则BE= .
,CD与OB交于点E,则BE= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,AD是⊙O的弦,点F是DA延长线的一点,AC平分∠FAB交⊙O于点C,过点C作CE⊥DF,垂足为点E.
(1)求证:CE是⊙O的切线;
(2)若AE=1,CE=2,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市重庆路水果市场某水果店购进甲、乙两种水果.已知1千克甲种水果的进价比1千克乙种水果的进价多4元,购进2千克甲种水果与1千克乙种水果共需20元.
(1)求甲种水果的进价为每千克多少元?
(2)经市场调查发现,甲种水果每天销售量y(千克)与售价m(元/千克)之间满足如图所示的函数关系,求y与m之间的函数关系;
(3)在(2)的条件下,当甲种水果的售价定为多少元时,才能使每天销售甲种水果的利润最大?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com