
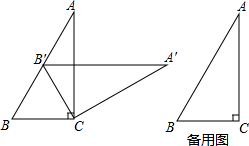
分析 (1)证得△B′BC为等边三角形即可得到∠B′CB=α=60°;
(2)分x=0、0<x≤1、1<x≤$\frac{3}{2}$、$\frac{3}{2}$<x≤2四种情况分类讨论得到重叠部分的面积即可.
解答 解:(1)∵∠ACB=90°,∠A=30°,
∴∠B=60°,
∵B′C=BC,
∴△B′BC为等边三角形,
∴∠B′CB=α=60°;
(2)如图①,
BC=AC tan30°=$\sqrt{3}$×$\frac{\sqrt{3}}{3}$=1=B′C,A′B′=AB=2,∠A′=∠A=30°.
由(1)得,∠B′CB=60°=∠B=∠BB′C.则△BB′C是等边三角形,AB′=1,
∴∠A′B′C=∠B′CB=60°,
∴A′B′∥BC.
∴B′D=$\frac{1}{2}$A′B′=$\frac{1}{2}$,A′D=$\frac{3}{2}$.S△A′B′C=S△ABC=$\frac{\sqrt{3}}{2}$.
当0<x≤1时,如图②.
由题知B′E=CC′=x.
则A′D=$\frac{3}{2}$-x,DG=($\frac{3}{2}$-x)•tan30°=$\frac{\sqrt{3}}{3}$($\frac{3}{2}$-x).
∴S△A′DG=$\frac{1}{2}$A′D-DG=$\frac{1}{2}$($\frac{3}{2}$-x)•$\frac{\sqrt{3}}{3}$($\frac{3}{2}$-x)=$\frac{\sqrt{3}}{6}$($\frac{3}{2}$-x)2.
同理可证:△B′EF是等边三角形.
∴S△B′EF=$\frac{1}{2}$B′E•B′F•sin60°=$\frac{1}{2}$×x×x×$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{4}$x2,
∴y=S△A′B′C-S△A′DG-S△B′EF=$\frac{\sqrt{3}}{2}$-$\frac{\sqrt{3}}{6}$($\frac{3}{2}$-x)2-$\frac{\sqrt{3}}{4}$x2
当1<x≤$\frac{3}{2}$时,如图③,
∵∠EMA′=∠AED-∠A′=30°=∠A′,
∴ME=A′E=2-x.
过点M做MN⊥A′B′,垂足为N.MN=ME sin∠MEN=$\frac{\sqrt{3}}{2}$(2-x).
∴S△A′EM=$\frac{1}{2}$(2-x)•$\frac{\sqrt{3}}{2}$(2-x)=$\frac{\sqrt{3}}{4}$(2-x)2.
∴y=S△A′EM-S△A′DG=$\frac{\sqrt{3}}{4}$(2-x)2-$\frac{\sqrt{3}}{6}$($\frac{3}{2}$-x)2=$\frac{\sqrt{3}}{12}$x2-$\frac{\sqrt{3}}{2}$x+$\frac{5\sqrt{3}}{8}$,
当$\frac{3}{2}$<x≤2时,如图④,
y=S△A′EM=$\frac{\sqrt{3}}{4}$(2-x)2=$\frac{\sqrt{3}}{4}$x2-$\sqrt{3}x$+$\sqrt{3}$.
∴综上y=$\left\{\begin{array}{l}{-\frac{5\sqrt{3}}{12}{x}^{2}+\frac{\sqrt{3}}{2}x+\frac{\sqrt{3}}{8}(0<x≤1)}\\{\frac{\sqrt{3}}{12}{x}^{2}-\frac{\sqrt{3}}{2}x+\frac{5\sqrt{3}}{8}(1<x≤\frac{3}{2})}\\{\frac{\sqrt{3}}{4}{x}^{2}-\sqrt{3}x+\sqrt{3}(\frac{3}{2}<x≤2)}\end{array}\right.$.
点评 考查了几何变换综合知识及相似三角形的知识,解题的关键是能够分类讨论确定重叠部分的面积,这也是中考的热点考点之一,有一定的难度,在平时的训练中应该加强训练,难度较大.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
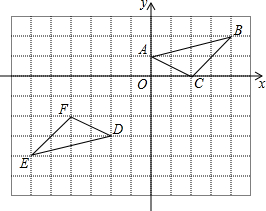 如图,在平面直角坐标系中,点A的坐标为(0,1),点B的坐标为(4,2),C的坐标为(2,0),将△ABC绕点P旋转180°得到△DEF,则旋转中心P点的坐标为(-1,-1).
如图,在平面直角坐标系中,点A的坐标为(0,1),点B的坐标为(4,2),C的坐标为(2,0),将△ABC绕点P旋转180°得到△DEF,则旋转中心P点的坐标为(-1,-1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
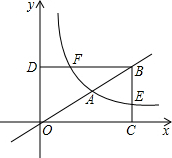 如图,A(2,1)是矩形OCBD的对角线OB上的一点,点E在BC上,双曲线y=$\frac{k}{x}$经过点A,交BC于点E,交BD于点F,若CE=$\frac{2}{3}$.
如图,A(2,1)是矩形OCBD的对角线OB上的一点,点E在BC上,双曲线y=$\frac{k}{x}$经过点A,交BC于点E,交BD于点F,若CE=$\frac{2}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,在直角三角形ABC中,已知AB=3cm,AC=4cm,BC=5cm,现将三角形ABC沿着垂直于BC的方向平移6cm,到三角形A′B′C′的位置.
如图所示,在直角三角形ABC中,已知AB=3cm,AC=4cm,BC=5cm,现将三角形ABC沿着垂直于BC的方向平移6cm,到三角形A′B′C′的位置.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
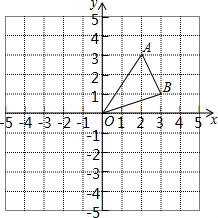 在平面直角坐标系中,点A(2,3)、B(3,1),O为坐标原点.
在平面直角坐标系中,点A(2,3)、B(3,1),O为坐标原点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,AB=AC,点D是边BC的中点,过点A、D分别作BC与AB的平行线,相交于点E,连结EC、AD.
如图,在△ABC中,AB=AC,点D是边BC的中点,过点A、D分别作BC与AB的平行线,相交于点E,连结EC、AD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com