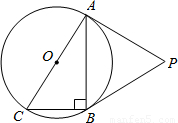
(2009•孝感)5月份,某品牌衬衣正式上市销售.5月1日的销售量为10件,5月2日的销售量为35件,以后每天的销售量比前一天多25件,直到日销售量达到最大后,销售量开始逐日下降,至此,每天的销售量比前一天少15件,直到5月31日销售量为0.设该品牌衬衣的日销量为p(件),销售日期为n(日),p与n之间的关系如图所示.
(1)写出p关于n的函数关系式p=______
【答案】
分析:(1)因为5月1日的销售量为10件,5月2日的销售量为35件,以后每天的销售量比前一天多25件,直到日销售量达到最大后,销售量开始逐日下降,至此,每天的销售量比前一天少15件,直到5月31日销售量为0,所以
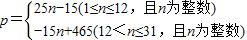
(2)分1≤n≤12时和12<n≤31两种情况列出不等式,分别求出n的取值范围即可;
(3)以12日为界,前后是两个等差数列 当 1≤n≤12时,首项a
1=10,末项a
12=285,项数 k
1=12 所以 和 s
1=(10+285)×
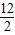
=1770 当 12<n≤31时,首项a
13=270,末项a
31=0,项数 k
2=19 所以 和 s
1=270×
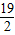
=2565,再求出其和即可.
解答:解:(1)此题的关键是销售量转折点日期的确定,设5月x日是最后一天销售量增加的日期,据题意,
有10+25(x-1)=15(31-x),解得 x=12,
因此(1)10+25(n-1),1≤n≤12;
p=15(31-n),12<n≤31.
故
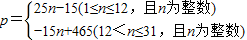
;
(2)当1≤n≤12时,若 10+25(n-1)>150解得 n>
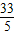
,
考虑实际日期,应从7日起算,此段时间流行期为12-7+1=6天,
当12<n≤31时,15(31-n)>150,解得 n<21,
故此段流行期为20-12=8天 因此,本月流行期为 6+8=14天;
(3)以12日为界,前后是两个等差数列
当1≤n≤12时,首项a
1=10,末项a
12=285,项数k
1=12,所以和s
1=(10+285)×
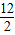
=1770
当12<n≤31时,首项a
13=270,末项a
31=0,项数 k
2=19 所以和s
1=270×
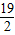
=2565,
所以本月共销售了1770+2565=4335件.
点评:本题需仔细观察图象,利用分段函数解决问题.

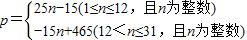
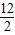 =1770 当 12<n≤31时,首项a13=270,末项a31=0,项数 k2=19 所以 和 s1=270×
=1770 当 12<n≤31时,首项a13=270,末项a31=0,项数 k2=19 所以 和 s1=270×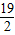 =2565,再求出其和即可.
=2565,再求出其和即可.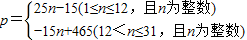 ;
;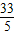 ,
,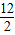 =1770
=1770 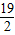 =2565,
=2565,

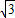 ,BC=1,求⊙O的半径.
,BC=1,求⊙O的半径.