
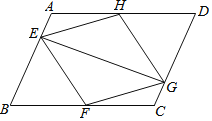
【题目】如图,在平行四边形ABCD中,点E,F,G,H分别在边AB,BC,CD,DA上,AE=CG,AH=CF,且EG平分∠HEF.
(1)求证:△AEH≌△CGF.
(2)若∠EFG=90°.求证:四边形EFGH是正方形.
【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)根据全等三角形的判定定理SAS证得结论;
(2)先证明四边形EFGH是平行四边形,再证明有一组邻边相等,然后结合∠EFG=90°,即可证得该平行四边形是正方形.
证明:(1)∵四边形ABCD是平行四边形,
∴∠A=∠C.
在△AEH与△CGF中,
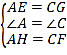 ,
,
∴△AEH≌△CGF(SAS);
(2)∵四边形ABCD是平行四边形,
∴AD=BC,AB=CD,∠B=∠D.
∵AE=CG,AH=CF,
∴EB=DG,HD=BF.
∴△BEF≌△DGH(SAS),
∴EF=HG.
又∵△AEH≌△CGF,
∴EH=GF.
∴四边形HEFG为平行四边形.
∴EH∥FG,
∴∠HEG=∠FGE.
∵EG平分∠HEF,
∴∠HEG=∠FEG,
∴∠FGE=∠FEG,
∴EF=GF,
又∵∠EFG=90°,
∴平行四边形EFGH是正方形.
∴四边形EFGH是菱形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知,点P是等边三角形△ABC中一点,线段AP绕点A逆时针旋转60°到AQ,连接PQ、QC.
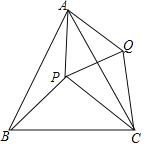
(1)求证:△BAP≌△CAQ.
(2)若PA=3,PB=4,∠APB=150°,求PC的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=﹣x2+bx+c的对称轴为直线x=2,且顶点在x轴上.
(1)求b、c的值;
(2)画出抛物线的简图并写出它与y轴的交点C的坐标;
(3)根据图象直接写出:点C关于直线x=2对称点D的坐标 ;若E(m,n)为抛物线上一点,则点E关于直线x=2对称点的坐标为 (用含m、n的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为落实“垃圾分类”,环卫部门要求垃圾要按A,B,C三类分别装袋,投放,其中A类指废电池,过期药品等有毒垃圾,B类指剩余食品等厨余垃圾,C类指塑料,废纸等可回收垃圾.甲投放了一袋垃圾,乙投放了两袋垃圾,这两袋垃圾不同类.
(1)直接写出甲投放的垃圾恰好是A类的概率;
(2)求乙投放的垃圾恰有一袋与甲投放的垃圾是同类的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() .
.
(1)求抛物线的解析式;
(2)点![]() 在抛物线的对称轴上,当
在抛物线的对称轴上,当![]() 的周长最小时,点
的周长最小时,点![]() 的坐标为_____________;
的坐标为_____________;
(3)点![]() 是第四象限内抛物线上的动点,连接
是第四象限内抛物线上的动点,连接![]() 和
和![]() .求
.求![]() 面积的最大值及此时点
面积的最大值及此时点![]() 的坐标;
的坐标;
(4)若点![]() 是对称轴上的动点,在抛物线上是否存在点
是对称轴上的动点,在抛物线上是否存在点![]() ,使以点
,使以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形?若存在,请直接写出点
为顶点的四边形是平行四边形?若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() 是
是![]() 的角平分线,
的角平分线,![]() ,
,![]() 在
在![]() 边上,以
边上,以![]() 为直径的半圆
为直径的半圆![]() 经过点
经过点![]() ,交
,交![]() 于点
于点![]() .
.

(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)已知![]() ,
,![]() 的半径为
的半径为![]() ,求图中阴影部分的面积.(最后结果保留根号和
,求图中阴影部分的面积.(最后结果保留根号和![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年,某贫困户的家庭年人均纯收入为2500元,通过政府产业扶持,发展了养殖业后,到2018年,家庭年人均纯收入达到了3600元.
(1)求该贫困户2016年到2018年家庭年人均纯收入的年平均增长率;
(2)若年平均增长率保持不变,2019年该贫困户的家庭年人均纯收入是否能达到4200元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解全校学生主题阅读的情况,随机抽查了部分学生在某一周主题阅读文章的篇数,并制成下列统计图表.
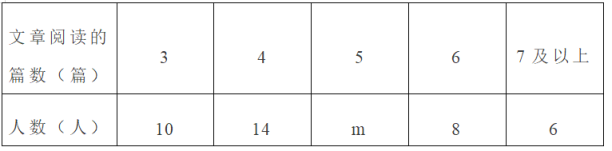

请根据统计图表中的信息,解答下列问题:
(1)求被抽查的学生人数和m的值;
(2)求本次抽查的学生文章阅读篇数的中位数和众数;
(3)若该校共有1200名学生,根据抽查结果,估计该校学生在这一周内文章阅读的篇数为4篇的人数。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com