
【题目】如图,在ABCD中,M、N分别是AD,BC的中点,∠AND=90°,连接CM交DN于点O.

(1)求证:△ABN≌△CDM;
(2)过点C作CE⊥MN于点E,交DN于点P,若PE=1,∠1=∠2,求AN的长.
【答案】(1)见解析;(2)2![]() .
.
【解析】
试题分析:(1)由四边形ABCD是平行四边形,可得AB=CD,AD=BC,∠B=∠CDM,又由M、N分别是AD,BC的中点,即可利用SAS证得△ABN≌△CDM;
(2)易求得∠MND=∠CND=∠2=30°,然后由含30°的直角三角形的性质求解即可求得答案.
(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,∠B=∠CDM,
∵M、N分别是AD,BC的中点,
∴BN=DM,
∵在△ABN和△CDM中,
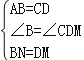 ,
,
∴△ABN≌△CDM(SAS);
(2)解:∵M是AD的中点,∠AND=90°,
∴MN=MD=![]() AD,
AD,
∴∠1=∠MND,
∵AD∥BC,
∴∠1=∠CND,
∵∠1=∠2,
∴∠MND=∠CND=∠2,
∴PN=PC,
∵CE⊥MN,
∴∠CEN=90°,
∠END+∠CNP+∠2=180°﹣∠CEN=90°
又∵∠END=∠CNP=∠2
∴∠2=∠PNE=30°,
∵PE=1,
∴PN=2PE=2,
∴CE=PC+PE=3,
∴CN=![]() =2
=2![]() ,
,
∵∠MNC=60°,CN=MN=MD,
∴△CNM是等边三角形,
∵△ABN≌△CDM,
∴AN=CM=2![]() .
.


科目:初中数学 来源: 题型:
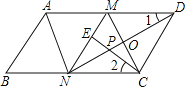
【题目】如图所示,四边形ABCD、DEFG都是正方形,连接AE、CG。
(1)求证:AE=CG;
(2)观察图形,猜想AE与CG之间的位置关系,并证明你的猜想。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设a,b是任意两个不等实数,我们规定:满足不等式a≤x≤b的实数x的所有取值的全体叫做闭区间,表示为[a,b],对于一个函数,如果它的自变量x与函数值y满足:当m≤x≤n时,有m≤y≤n,我们就称此函数是闭区间[m,n]上的“闭函数”.
(1)反比例函数y=![]() 是闭区间[1,2015]上的“闭函数”吗?请判断并说明理由;
是闭区间[1,2015]上的“闭函数”吗?请判断并说明理由;
(2)若一次函数y=kx+b(k>0)是闭区间[m,n]上的“闭函数”,求此函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
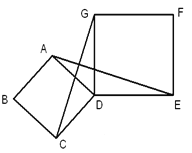
【题目】如图,△ABC中,以AB为直径的⊙O交AC于点D,∠DBC=∠BAC.
(1)求证:BC是⊙O的切线;
(2)若⊙O的半径为2,∠BAC=30°,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB于点D.点P从点D出发,沿线段DC向点C运动,点Q从点C出发,沿线段CA向点A运动,两点同时出发,速度都为每秒1个单位长度,当点P运动到C时,两点都停止.设运动时间为t秒.
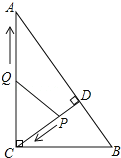
(1)求线段CD的长;
(2)设△CPQ的面积为S,求S与t之间的函数关系式,并确定在运动过程中是否存在某一时刻t,使得S△CPQ:S△ABC=9:100?若存在,求出t的值;若不存在,则说明理由.
(3)是否存在某一时刻t,使得△CPQ为等腰三角形?若存在,求出所有满足条件的t的值;若不存在,则说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各组数中,具有相反意义的量是( )
A. 身高180cm和身高90cm B. 向东走5公里和向南走5公里
C. 收入300元和支出300元 D. 使用汽油10公斤和浪费酒精10公斤
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com