
分析 先根据分式混合运算的法则把原式进行化简,再把求出x、y的值代入进行计算即可.
解答 解:原式=($\frac{2x}{2x+y}$-$\frac{4{x}^{2}}{(2x+y)^{2}}$)÷$\frac{-y}{(2x-y)(2x+y)}$
=$\frac{2xy}{{(2x+y)}^{2}}$•$\frac{(2x-y)(2x+y)}{-y}$
=-$\frac{2x(2x-y)}{2x+y}$,
解方程组$\left\{\begin{array}{l}{2x-y=3}\\{3x+2y=8}\end{array}\right.$得$\left\{\begin{array}{l}x=2\\ y=1\end{array}\right.$,
故原式=-$\frac{4×(4-1)}{4+1}$=-$\frac{12}{5}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
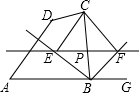 如图,在四边形ABCD中,点P是边BC上一动点,过点P作直线EF∥AB,且与∠ABC、∠CBG的角平分线分别相交于点E、F.
如图,在四边形ABCD中,点P是边BC上一动点,过点P作直线EF∥AB,且与∠ABC、∠CBG的角平分线分别相交于点E、F.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3,4,5 | B. | 5,12,13 | C. | $\sqrt{2},\sqrt{2},2$ | D. | 1,2,3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,已知三角形ABC平移后得到三角形DEF,则下列说法中,不正确的是( )
如图,已知三角形ABC平移后得到三角形DEF,则下列说法中,不正确的是( )| A. | AC=DF | B. | BC∥EF | ||
| C. | 平移的距离是线段BD的长 | D. | 平移的距离是线段AD的长 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
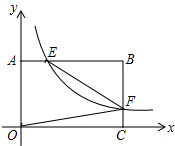 如图,反比例函数y=$\frac{k}{x}$(x>0)的图象与矩形OABC的边AB、BC分别交于点E、F,若S矩形OABC=2,则当k=1时,四边形OAEF的面积最大.
如图,反比例函数y=$\frac{k}{x}$(x>0)的图象与矩形OABC的边AB、BC分别交于点E、F,若S矩形OABC=2,则当k=1时,四边形OAEF的面积最大.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com