
 甲、乙两列火车分别从A、B两城同时匀速开出,甲车开往B城,乙车开往A城.由于墨迹覆盖,甲车与乙车据B城的距离s(千米)与时间t(小时)的函数关系部分图象如图所示.
甲、乙两列火车分别从A、B两城同时匀速开出,甲车开往B城,乙车开往A城.由于墨迹覆盖,甲车与乙车据B城的距离s(千米)与时间t(小时)的函数关系部分图象如图所示.分析 (1)根据图象可得甲车的速度为(420-60)÷(3-1)解答即可,得出甲的函数关系式,把x=0代入解答即可;
(2)让两个函数解析式的y相等即可求得两车相遇时t的值;
(3)让甲的函数关系式减去乙的函数关系式为300或乙的函数关系式减去甲的函数关系式为300即可求得所求的时间.
解答 解:(1)由图象可知:甲车的速度为(420-60)÷(3-1)=180千米/小时,
设s甲与t的函数关系为s甲=k1t+b,
∵图象过点(3,60)与(1,420),
∴$\left\{\begin{array}{l}{3{k}_{1}+b=60}\\{{k}_{1}+b=420}\end{array}\right.$,
解得$\left\{\begin{array}{l}{{k}_{1}=-180}\\{{b}_{1}=600}\end{array}\right.$,
∴s甲与t的函数关系式为s甲=-180t+600;
把x=0代入s甲=-180t+600=600,
可得A、B两地相距600千米;
故答案为:180;600;
(2)设s乙与t的函数关系式为s乙=k2t,
∵图象过点(1,120),
∴k2=120.
∴s乙与t的函数关系式为s乙=120t
∵s甲=s乙,即-180t+600=120t,解得t=2.
∴当t=2时,两车相遇;
(3)当相遇前两车相距300千米时,s甲-s乙=300,
即-180t+600-120t=300,解得t=1.
当相遇后两车相距300千米时,s乙-s甲=300,
即 120t+180t-600=300.
解得t=3.
综上所述,当t等于1或3小时时,两车相距300千米.
点评 考查用待定系数法求一次函数解析式以及一次函数解析式的应用;得到两个函数的关系式是解决本题的突破点;用数形结合的方法判断出所求值与得到函数关系式的关系是解决本题的难点.


 优学名师名题系列答案
优学名师名题系列答案科目:初中数学 来源: 题型:选择题
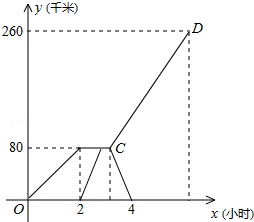 已知:A、B两市相距260千米,甲车从A市前往B市运送物资,行驶2小时在M地汽车出现故障,立即通知技术人员乘乙车从A市赶来维修(通知时间忽略不计),乙车到达M地后又经过20分钟修好甲车后以原速原路返回,同时甲车以原速1.5倍的速度前往B市,如图是两车距A市的路程y(千米)与甲车行驶时间x(小时)之间的函数图象,由图象信息得出如下结论:①甲车提速后的速度是60千米/时;②乙车的速度是96千米/时;③点C的坐标为($\frac{19}{6}$,80);④甲车到达B市时乙车已返回A市2小时.你认为正确的结论有( )个.
已知:A、B两市相距260千米,甲车从A市前往B市运送物资,行驶2小时在M地汽车出现故障,立即通知技术人员乘乙车从A市赶来维修(通知时间忽略不计),乙车到达M地后又经过20分钟修好甲车后以原速原路返回,同时甲车以原速1.5倍的速度前往B市,如图是两车距A市的路程y(千米)与甲车行驶时间x(小时)之间的函数图象,由图象信息得出如下结论:①甲车提速后的速度是60千米/时;②乙车的速度是96千米/时;③点C的坐标为($\frac{19}{6}$,80);④甲车到达B市时乙车已返回A市2小时.你认为正确的结论有( )个.| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某农户种植一种经济作物,总量用水量y(m3)与种植时间x(天)之间的函数关系如图所示.
某农户种植一种经济作物,总量用水量y(m3)与种植时间x(天)之间的函数关系如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 甲、乙两地之间有一条笔直的公路L,小明从甲地出发沿公路L步行前往乙地,同时小亮从乙地出发沿公路L骑自行车前往甲地,小亮到达甲地停留一段时间,原路原速返回,追上小明后两人一起步行到乙地.设小明与甲地的距离为y1米,小亮与甲地的距离为y2米,小明与小亮之间的距离为s米,小明行走的时间为x分钟.y1、y2与x之间的函数图象如图1,s与x之间的函数图象(部分)如图.
甲、乙两地之间有一条笔直的公路L,小明从甲地出发沿公路L步行前往乙地,同时小亮从乙地出发沿公路L骑自行车前往甲地,小亮到达甲地停留一段时间,原路原速返回,追上小明后两人一起步行到乙地.设小明与甲地的距离为y1米,小亮与甲地的距离为y2米,小明与小亮之间的距离为s米,小明行走的时间为x分钟.y1、y2与x之间的函数图象如图1,s与x之间的函数图象(部分)如图.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
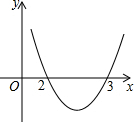 已知二次函数y=x2-5x+6,当自变量x取m时,对应的函数值小于0,当自变量x取m-1、m+1时,对应的函数值为y1、y2,则y1、y2满足( )
已知二次函数y=x2-5x+6,当自变量x取m时,对应的函数值小于0,当自变量x取m-1、m+1时,对应的函数值为y1、y2,则y1、y2满足( )| A. | y1>0,y2>0 | B. | y1<0,y2>0 | C. | y1<0,y2<0 | D. | y1>0,y2<0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com