
����Ŀ�� ����������ǰ��ij��Ҷ����������ɽ�賧�Ⱥ�������Ҷ����һ����Ҷ��������5.4��Ԫ����������ΪaԪ/ǧ�ˣ����غ�������̽���Ҷ�����װ���ۣ�������300ǧ�˾�װƷ�Խ����������������ۣ����µļ�װƷ��150Ԫ/ǧ�˵ļ۸���ۣ�ȫ���������ڶ�����������5��Ԫ����һ�εĽ�������ÿǧ�˱ȵ�һ������20Ԫ�����ط����װ��װƷռ��������һ�룬��200Ԫ/ǧ�˵ĵ��۳��ۣ����µļ�װƷ�������������۵Ļ�����ÿǧ�˼Ӽ�40Ԫ��ȫ���������������ɱ����ƣ��ڶ�����Ҷ��õ�ë������3.5��Ԫ��
��1���ú�a�Ĵ���ʽ��ʾ��һ����Ҷ��ë����
��2�����һ����Ҷ�о�װƷÿǧ���ۼۣ������ۼ�-�ܽ���=ë����
���𰸡���1��600a+![]() -99000����2��240Ԫ
-99000����2��240Ԫ
��������
��1���������۶��ȥ�ɱ��������ë����
��2����Ϊ��һ����������Ϊ![]() Ԫ/ǧ�ˣ���ڶ����Ľ�������Ϊ(
Ԫ/ǧ�ˣ���ڶ����Ľ�������Ϊ(![]() )Ԫ/ǧ�ˣ����ݵڶ�����Ҷ��õ�ë������35000Ԫ���з�����⣮
)Ԫ/ǧ�ˣ����ݵڶ�����Ҷ��õ�ë������35000Ԫ���з�����⣮
��1��������ã���һ����Ҷ��ë����Ϊ��
300��2a+150��(![]() -300)-54000=600a+
-300)-54000=600a+![]() 99000��
99000��
��2�����һ����������ΪaԪ/ǧ�ˣ�
������ã�![]() ��
��![]() ��200+
��200+![]() ��
��![]() ��(
��(![]() 20+40)
20+40)![]() 50000=35000��
50000=35000��
��ã�![]() 120��
120��
�����飺![]() 120��ԭ��ʽ���̵Ľ⣬�ҷ������⣮
120��ԭ��ʽ���̵Ľ⣬�ҷ������⣮
���ۼ�Ϊ��![]() ��
��
�𣺵�һ����Ҷ�о�װƷÿǧ���ۼ�Ϊ240Ԫ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
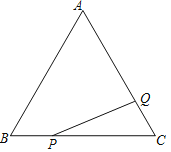
����Ŀ����ͼ����֪�ȱߡ�ABC�ı߳�Ϊ4����P��Q�ֱ��DZ�BC��AC��һ�㣬PB��1����PA��_____����BQ��AP����AQ��_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y��ax2��bx��c��a��0����ͼ����ͼ��ʾ��������5�����ۣ� �� c=0���ڸ������ߵĶԳ�����ֱ��x=��1���۵�x=1ʱ��y=2a����am![]() +bm+a��0��m����1��������A��100��y����B����100��y
+bm+a��0��m����1��������A��100��y����B����100��y![]() ���ڸ�������������y��y
���ڸ�������������y��y![]() ��������ȷ�Ľ�����___________ ����д��������ȷ���۵���ţ�
��������ȷ�Ľ�����___________ ����д��������ȷ���۵���ţ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
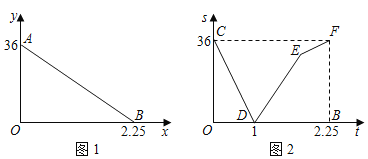
����Ŀ��С���Ӽҳ�����һ����ֱ�Ĺ�·�����г�ǰ��ͼ��ݿ��飬����ͼ���֮��ľ���y��km�������ʱ��t��h��֮��ĺ�����ϵ��ͼ1���߶�AB��ʾ����С��������ͬʱ��С���������ͼ��ݽ����������ͬһ����·��綯�����ٻؼң�����֮��ľ���s��km�������ʱ��t��h��֮��ĺ�����ϵʽ��ͼ2�����߶�CD��DE��EF��ʾ��
��1��С�������г����ٶ�Ϊ�� ��km/h��������綯�����ٶ�Ϊ�� ��km/h��
��2������ͼ�е�E��ʵ�����壬�������E�����ꣻ
��3����tΪ����ʱ������֮��ľ���Ϊ18km��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�� С����������һ������
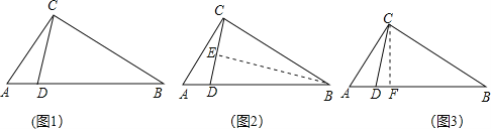
��ͼ1����ABC�У���ACB=90������D��AB�ϣ���BD=BC����֤����ABC=2��ACD��
С�����֣�����ֱ���ýǶȼ���ķ����⣬���������������ַ�����
����2����ͼ2����BE��CD������Ϊ��E��
����3����ͼ3����CF��AB������Ϊ��F��
�����Ķ����ϣ������ַ�������ѡһ�ַ�����֤����ABC=2��ACD��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������������ABC�У���D��E�ֱ��ڱ�AC��AB�ϣ�AG��BC�ڵ�G��AF��DE�ڵ�F����EAF=��GAC��
��1����֤����ADE�ס�ABC��
��2����AD=3��AB=5����![]() ��ֵ��
��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����ƽ��ֱ������ϵxOy�У�A��0��4����B��8��0����C��8��4����
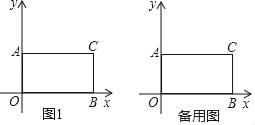
��1����˵���ı���AOBC�Ǿ��Σ�
��2����x����ȡһ��D������DCB�Ƶ�C˳ʱ����ת90��õ���D'CB'����D'���D��Ӧ����
����OD��3�����D'�����꣮
������AD'��OD'����AD'+OD'�Ƿ������Сֵ�������ڣ���ֱ��д����Сֵ����ʱ��D'�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
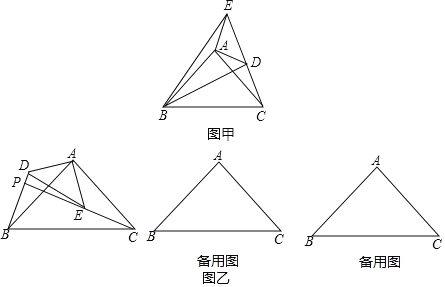
����Ŀ����ͼ�ң���ABC �͡�ADE ���й�������ĵ���ֱ�������Σ���BAC=��DAE=90�㣬��PΪ���� BD��CE�Ľ��㣮
��1����ͼ�ף�����ADE �Ƶ�A ��ת���� C��D��E ��ͬһ��ֱ����ʱ������BD��BE�������и������ĸ������У�������ȷ�����ļ��������ش�ֱ��д��ţ�
��BD=CE����BD��CE���ۡ�ACE+��DBC=45�㣻��BE2=2(AD2+AB2)
��2���� AB=4��AD=2���ѡ�ADE �Ƶ� A ��ת��
�ٵ���CAE=90��ʱ���� PB �ij���
��ֱ��д����ת�������߶� PB �������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ʵ��̽����
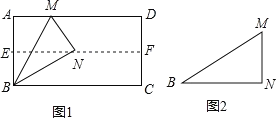
(1)��ͼ1�����۾���ֽƬABCD��ʹAD��BC�غϣ��õ��ۺ�EF����ֽƬչ������һ���۵�ֽƬ��ʹ��A����EF�ϣ���ʹ�ۺ۾�����B���õ��ۺ�BM��ͬʱ�õ��߶�BN��MN.����۲�ͼ1�������MBN�Ķ����Ƕ��٣���֤����Ľ���.
(2)��ͼ1�е�������ֽƬBMN���£���ͼ2���۵���ֽƬ��̽��MN��BM��������ϵ��д���۵�����������Ϸ���֤����Ľ���.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com