
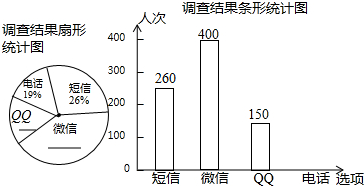
分析 (1)根据:总人次=“短信”人数÷“短信”占总数的百分比,计算可得;
(2)根据:各项目占总数的百分比=各项目的数量÷总数,分别计算出“微信”、“QQ”所占百分比及“电话”的人次数即可补全统计图;
(3)以“微信”中奖的比例乘以短信和QQ方式共获奖的人数即可.
解答 解:(1)参与这项有奖活动的观众共有:260÷26%=1000(人次);
(2)“微信”所占百分比:$\frac{400}{1000}$×100%=40%,
“QQ”所占百分比:$\frac{150}{1000}$×100%=15%,
“电话”的人数为:1000×19%=190(人次),
补全图形如图: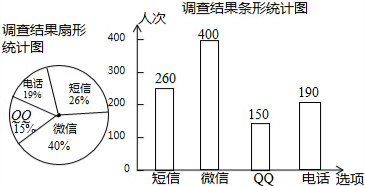
(3)(260+150)×$\frac{40}{400}$=41(人次),
答:估计通过短信和QQ方式共获奖41人次.
故答案为:(1)1000.
点评 本题考查了条形统计图和扇形统计图,条形统计图考查每组里面具体的人数,扇形统计图考查部分占整体的百分比,关键是能根据条形统计图和扇形统计图获得有关数据.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | (0,-$\frac{5}{9}$) | B. | ($\frac{7}{9}$,0) | C. | (0,$\frac{5}{9}$) | D. | (-$\frac{5}{9}$,0) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
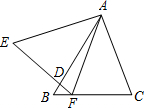 如图,△ABC与△AEF中,AB=AE,BC=EF,∠B=∠E,AB交EF于D.给出下列结论:
如图,△ABC与△AEF中,AB=AE,BC=EF,∠B=∠E,AB交EF于D.给出下列结论:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com