
����Ŀ�� ����һ��ǰϦ�ʼಿ�Ŵ�ij���о����Ķ�ͯ��ߡ�ͯ����ͯװ�й������300����ͯ��Ʒ�������Ǹ��ݳ�������Ƴ��IJ�������ͳ�Ʊ�������ͼ��
��� | ��ͯ��� | ͯ�� | ͯװ |
������ | 90 |

���������ͳ�Ʊ��������ṩ����Ϣ������������⣺
��1���ֱ�ȫ����ͳ�Ʊ���ͳ��ͼ��
��2����֪�����Ķ�ͯ��ߡ�ͯ����ͯװ�ĺϸ��ʷֱ�Ϊ90%��88%��80%�����Ӹó��е��������ͯ��Ʒ���������һ�����ϸ�Ʒ�ĸ����Ƕ��٣�
���𰸡���1�����������2��85��
��������
��1������ͯ����������300��25%��ͯװ��������300��75��90����ͯ���ռ�ðٷֱ���90��300
��100%��ͯװռ�ðٷֱ�1��30%��25%�����ɲ�ȫͳ�Ʊ���ͳ��ͼ��
��2���ȷֱ������ͯ��ߡ�ͯ����ͯװ�кϸ������֮�ͣ��ٸ��ݸ��ʹ�ʽ���㼴�ɣ�
�⣺��1��ͯ����������300��25%=75��ͯװ��������300��75��90=135��
��ͯ���ռ�ðٷֱ��ǣ�90��300����100%=30%��ͯװռ�ðٷֱ�1��30%��25%=45%��
��ȫͳ�Ʊ���ͳ��ͼ���£�
��� | ��ͯ��� | ͯ�� | ͯװ |
������ | 90 | 75 | 135 |

��2������ͯ����кϸ��������90��90%=81��ͯ���кϸ��������75��88%=66��ͯװ�кϸ��������135��80%=108��
���Ӹó��е��������ͯ��Ʒ���������һ�������ϸ�Ʒ�ĸ�����
![]() ��
��


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Ϊ���������ߵĶ��κ����ı���ʽ��
��1��������y��ax2+bx+2�����㣨��2��6������2��2����
��2�������ߵĶ�������Ϊ��3����5�����������߾����㣨0��1����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��۳�����ijƷ�Ƶ���۰�������5�����Σ�������һ������͵��Σ���ۣ�ÿ��������55�֣�ÿ������1000Ԫ.������۵�����ÿ���һ�����Σ�ÿ�����������200Ԫ����ÿ��IJ��������5��.
��1����������![]() ���ε����ÿ���������Ϊ
���ε����ÿ���������Ϊ![]() Ԫ������
Ԫ������![]() Ϊ����������
Ϊ����������![]() �����������ĸ����ε����ʱ��ÿ����������ÿ�����������Ƕ���Ԫ��
�����������ĸ����ε����ʱ��ÿ����������ÿ�����������Ƕ���Ԫ��
��2����������![]() ���ε����һ���������Ϊ60000Ԫ�������۵���������.
���ε����һ���������Ϊ60000Ԫ�������۵���������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��![]() �ǵȱ������Σ���P��
�ǵȱ������Σ���P��![]() ���ӳ����ϣ���PΪ���ģ����߶�
���ӳ����ϣ���PΪ���ģ����߶�![]() ��ʱ����תn�㣨
��ʱ����תn�㣨![]() �����߶�
�����߶�![]() ������
������![]() ��
��![]() ��
��

��1����ͼ����![]() ��������
��������![]() ʱ��ͼ�Σ���д����ʱn��ֵ��
ʱ��ͼ�Σ���д����ʱn��ֵ��
��2��MΪ�߶�![]() ���е㣬����
���е㣬����![]() ��д��һ��n��ֵ��ʹ�ö���
��д��һ��n��ֵ��ʹ�ö���![]() �ӳ���������һ��P������
�ӳ���������һ��P������![]() ����˵�����ɣ�
����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
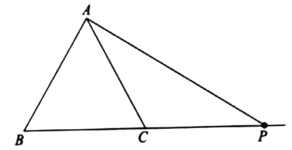
����Ŀ����ͼ����֪��C����ABΪֱ���ġ�O��һ�㣬CH��AB�ڵ�H������B����O�����߽�ֱ��AC�ڵ�D����EΪCH���е㣬����AE���ӳ���BD�ڵ�F��ֱ��CF��AB���ӳ�����G��
��1����֤��FC��FB��
��2����֤��CG�ǡ�O�����ߣ�
��3����FB��FE��2�����O�İ뾶��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
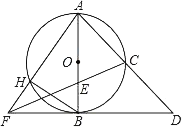
����Ŀ����ͼ����Rt��ABC�У���C��90������CAB��ƽ���߽�BC�ڵ�D��DEǡ����AB�Ĵ�ֱƽ���ߣ�����ΪE����BC��6����AB�ij�Ϊ��������

A.3![]() B.4
B.4![]() C.8D.10
C.8D.10
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������y����![]() x2+bx+c��x�ύ��ԭ��O�͵�A��6��0���������ߵĶ���ΪB��
x2+bx+c��x�ύ��ԭ��O�͵�A��6��0���������ߵĶ���ΪB��

��1����������ߵĽ���ʽ�Ͷ���B�����ꣻ
��2��������P��ԭ��O��������ÿ��1�����ȵ�λ���ٶ����߶�OB�˶������P�˶���ʱ��Ϊt��s�����ʵ�tΪ��ֵʱ����OPA��ֱ�������Σ�
��3����ͬʱ��һ����M�ӵ�A��������2�����ȵ�λ���ٶ����߶�AO�˶�����P��M����һ����ֹͣ�˶�ʱ��һ����Ҳ��ֹ֮ͣ�˶��������ǵ��˶�ʱ��Ϊt��s��������MP����tΪ��ֵʱ���ı���ABPM�������С���������Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
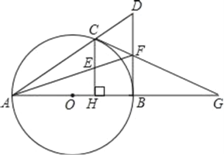
����Ŀ����ͼ��AB�ǡ�O��ֱ������C��![]() ���е㣬����AC���ӳ�����D��ʹCD��AC����E��OB��һ�㣬��
���е㣬����AC���ӳ�����D��ʹCD��AC����E��OB��һ�㣬��![]() ��CE���ӳ��߽�DB���ӳ����ڵ�F��AF����O�ڵ�H������BH��
��CE���ӳ��߽�DB���ӳ����ڵ�F��AF����O�ڵ�H������BH��
��1����֤��BD�ǡ�O�����ߣ���2����OB��2ʱ����BH�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() �ǵȱ������Σ���
�ǵȱ������Σ���![]() ��
��![]() �ֱ���
�ֱ���![]() �ϣ���
�ϣ���![]() ��
��![]() ��
��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() .
.
��1����֤��![]() ��
��
��2����ͼ2����![]() ��ֱ��
��ֱ��![]() ���۵õ���Ӧ��
���۵õ���Ӧ��![]() ������
������![]() ��
��![]() ��������
��������![]() �ڵ�
�ڵ�![]() ��
��![]() ��
��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ������
������![]() .
.
�����ж��ı���![]() ����״����˵������.
����״����˵������.
�����ı���![]() �����Ϊ
�����Ϊ![]() ��
��![]() ����
����![]() �ij�.
�ij�.
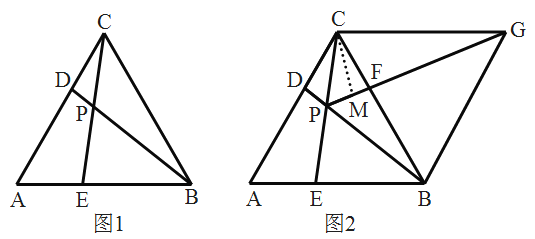
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com