Question

如图，梯形ABCD中，AD∥BC，∠ABC＝90°，AD＝9，BC＝12，AB＝a，在线段BC上任取一点P，连结DP，作射线PE⊥DP，PE与直线AB交于点E．

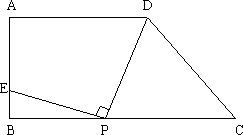
(1)试确定CP＝3时，点E的位置；

(2)若设CP＝x，BE＝y，试写出y关于自变量x的函数关系式；

(3)若在线段BC上能找到不同的两点P₁，P₂，使按上述作法得到的点E都与点A重合，试求出此时a的取值范围．

Answer 1

答案：
解析：

解：(1)作DF⊥BC，F为垂足 　　当CP＝3时 　　∵四边形ADFB是矩形，则CF＝3 　　∴点P与F重合 　　又BF⊥FD 　　∴此时点E与点B重合 　　(2)当点P在BF上时 　　∵∠EPB＋∠DPF＝90° 　　∠EPB＋∠PEB＝90° 　　∴∠DPF＝∠PEB 　　因而Rt△PEB∽△DPF，∴　　① 　　又BE＝y，BP＝12－x，FP＝x－3，FD＝a 　　代入①得 　　∴ 　　　　② 　　当点P在CF上时，可求得 　　(3)当点E与A重合时，y＝EB＝a，此时点P在线段BF上 　　由②得： 　　整理得：　　③ 　　由于在线段BC上能找到两个不同的点P1与P2满足条件，也就是说明方程③有两个不相等的正根 　　故有 　　解得：，又a＞0，∴0＜a＜