
如图,一次函数y=kx+1(k≠0)与反比例函数 (m≠0)的图象有公共点A(1,2).直线l⊥x轴于点N(3,0),与一次函数和反比例函数的图象分别交于点B,C.
(m≠0)的图象有公共点A(1,2).直线l⊥x轴于点N(3,0),与一次函数和反比例函数的图象分别交于点B,C.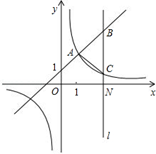
(1)求一次函数与反比例函数的解析式;
(2)求△ABC的面积?
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:初中数学 来源: 题型:解答题
如图,直线y=- x+8与x轴、y轴分别相交于点A、B,设M是OB上一点,若将△ABM沿AM折叠,使点B恰好落在x轴上的点B'处.
x+8与x轴、y轴分别相交于点A、B,设M是OB上一点,若将△ABM沿AM折叠,使点B恰好落在x轴上的点B'处.
求: (1)点B'的坐标: .(2分)
(2)直线AM所对应的函数关系式.(8分)
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知y+3与x+2成正比例,且当x=3时,y=7.
(1)写出y与x之间的函数关系式;
(2)当x=-1时,求y的值;
(3)当y=0时,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
某物体从P点运动到Q点所用时间为7秒,其运动速度v(米每秒)关于时间t(秒)的函数关系如图所示.某学习小组经过探究发现:该物体前进3秒运动的路程在数值上等于矩形AODB的面积.由物理学知识还可知:该物体前t(3<t≤7)秒运动的路程在数值上等于矩形AODB的面积与梯形BDNM的面积之和.
根据以上信息,完成下列问题:
(1)当3<t≤7时,用含t的式子表示v;
(2)分别求该物体在0≤t≤3和3<t≤7时,运动的路程s(米)关于时间t(秒)的函数关系式;
(3)求该物体从P点运动到Q总路程的 时所用的时间.
时所用的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
某商场销售甲、乙两种品牌的智能手机,这两种手机的进价和售价如下表所示:
| | 甲 | 乙 |
| 进价(元/部) | 4000 | 2500 |
| 售价(元/部) | 4300 | 3000 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
某服装店以每件40元的价格购进一批衬衫,在试销过程中发现:每月销售量y(件)与销售单价x(x为正整数)(元)之间符合一次函数关系,当销售单价为55元时,月销售量为140件;当销售单价
为70元时,月销售量为80件.
(1)求y与x的函数关系式;
(2)如果每销售一件衬衫需支出各种费用1元,设服装店每月销售该种衬衫获利为w元,求w与x之间的函数关系式,并求出销售单价定为多少元时,商场获利最大,最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,反比例函数 与一次函数y=x+b的图象,都经过点A(1,2)
与一次函数y=x+b的图象,都经过点A(1,2)
(1)试确定反比例函数和一次函数的解析式;
(2)求一次函数图象与两坐标轴的交点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
甲乙两车分别从A、B两地相向而行,甲车出发1小时后乙车出发,并以各自速度匀速行驶,两车相遇后依然按照原速度原方向各自行驶,如图所示是甲乙两车之间的距离S(千米)与甲车出发时间t(小时)之间的函数图象,其中D点表示甲车到达B地,停止行驶.
(1 )A、B两地的距离 千米;乙车速度是 ;a表示 .
(2)乙出发多长时间后两车相距330千米?
查看答案和解析>>
科目:初中数学 来源: 题型:单选题
抛物线y=﹣2x2经过平移到y=﹣2x2﹣4x﹣5,平移方法是( )
| A.向左平移1个单位,再向上平移3各单位 |
| B.向左平移1个单位,再向下平移3个单位 |
| C.向右平移1个单位,再向上平移3个单位 |
| D.向右平移1个单位,再向下平移3个单位 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com