
【题目】如图,对称轴为直线x=2的抛物线y=x2+bx+c与x轴交于点A和点B,与y轴交于点C,且点A的坐标为(﹣1,0)
(1)求抛物线的解析式;
(2)直接写出B、C两点的坐标;
(3)求过O,B,C三点的圆的面积.(结果用含π的代数式表示)
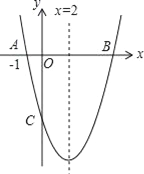
【答案】(1)y=x2﹣4x﹣5;(2)B(5,0),C(0,﹣5);(3)![]() π.
π.
【解析】试题分析:(1)利用对称轴方程可求得b,把点A的坐标代入可求得c,可求得抛物线的解析式;(2)根据A、B关于对称轴对称可求得点B的坐标,利用抛物线的解析式可求得B点坐标;(3)根据B、C坐标可求得BC长度,由条件可知BC为过O、B、C三点的圆的直径,可求得圆的面积.
试题解析:(1)由A(﹣1,0),对称轴为x=2,可得 ,解得
,解得![]() ,
,
∴抛物线解析式为y=x2﹣4x﹣5;
(2)由A点坐标为(﹣1,0),且对称轴方程为x=2,可知AB=6,
∴OB=5,
∴B点坐标为(5,0),
∵y=x2﹣4x﹣5,
∴C点坐标为(0,﹣5);
(3)如图,连接BC,则△OBC是直角三角形,

∴过O、B、C三点的圆的直径是线段BC的长度,
在Rt△OBC中,OB=OC=5,
∴BC=5![]() ,
,
∴圆的半径为![]() ,
,
∴圆的面积为π(![]() )2=
)2=![]() π.
π.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,BD为对角线,点P从A出发,沿射线AB运动,连接PD,过点D作DE⊥PD,交直线BC于点E.

(1)当点P在线段AB上时(如图1),求证:BP+CE=![]() BD;
BD;
(2)当点P在线段AB的延长线上时(如图2),猜想线段BP、CE、BD之间满足的关系式,并加以证明;
(3)若直线PE分别交直线BD、CD于点M、N,PM=3,EN=4,求PD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a,b,c分别是△ABC的三边长,且满足2a4+2b4+c4=2a2c2+2b2c2,则△ABC是( )
A. 等腰三角形 B. 等腰直角三角形
C. 直角三角形 D. 等腰三角形或直角三角形
【答案】B
【解析】解析:∵2a4+2b4+c4=2a2c2+2b2c2,∴4a4-4a2c2+c4+4b4-4b2c2+c4=0,
∴(2a2-c2)2+(2b2-c2)2=0,∴2a2-c2=0,2b2-c2=0,
∴c=2a,c=2b,
∴a=b,且a2+b2=c2,
∴△ABC为等腰直角三角形.
故选B.
【题型】单选题
【结束】
11
【题目】将图1中阴影部分的小长方形变换到图2的位置,你能根据两个图形的面积关系得到的数学公式是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《深圳都市报》报道,截止到2017年3月底,深圳共享单车注册用户量超千万人,互联网自行车日均使用量2590000人次,将2590000用科学记数法表示应为
A.0. 259×107
B.2.59×106
C.29.5×105
D.259×104
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查中,最适合采用抽样调查的是( )
A.乘坐高铁对旅客的行李的检查
B.了解全校师生对实验学校30周年校庆文艺表演节目的满意程度
C.调查初中2017级5班全体同学的身高情况
D.对新研发的新型战斗机的零部件进行检查
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列运算正确的是( )
A.(a+1)2=a2+1B.(a-b)3(b-a)2=(a-b)5C.(﹣2ab2)3=8a3b6 D.2x3x2=x6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形 ABCD 的对角线 AC 与 BD 相交于点 O,CE∥BD, DE∥AC , AD=2![]() , DE=2,则四边形 OCED 的面积为( )
, DE=2,则四边形 OCED 的面积为( )

A. 2![]() B. 4 C. 4
B. 4 C. 4![]() D. 8
D. 8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com