
若一元二次方程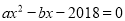 有一根为
有一根为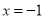 ,则
,则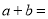 __________.
__________.
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案科目:初中数学 来源:2017-2018学年黑龙江省大庆市杜尔伯特县九年级(上)期末数学试卷(五四学制) 题型:单选题
二次函数y=ax2+bx+c(a≠0)的大致图象如图所示(1<x=h<2,0<xA<1),下列结论:① 2a+b>0;② abc<0;③ 若OC=2OA,则2b-ac = 4;④ 3a﹣c<0,其中正确的个数是( )
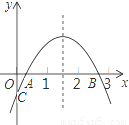
A. 1 B. 2 C. 3 D. 4
C 【解析】试题解析:①∵抛物线的开口向下, ∴a<0. ∵抛物线的对称轴->1, ∴b>-2a,即2a+b>0,①成立; ②∵b>-2a,a<0, ∴b>0, ∵抛物线与y轴的交点在y轴的负半轴, ∴c<0, ∴abc>0,②错误; ③点A的横坐标为,点C的纵坐标为c, ∵OC=2OA, ∴-c=,整理得:2b-ac=4,③...查看答案和解析>>
科目:初中数学 来源:山东省德州地区2017-2018学年度第一学期期末检测八年级数学试卷 题型:填空题
已知4y2+my+1是完全平方式,则常数m的值是_________
4和-4 【解析】试题解析:∵4y2-my+1是完全平方式, ∴-m=±4,即m=±4. 故答案为:4和-4查看答案和解析>>
科目:初中数学 来源:广东省汕头市澄海区2018届九年级上学期期末质量检测数学试卷 题型:解答题
如图,⊙O是△ABC的外接圆,∠ABC=45°,AD是⊙O的切线交BC的延长线于D,AB交OC于E.
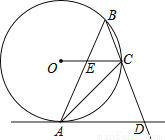
(1)求证:AD∥OC;
(2)若AE=2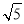 ,CE=2.求⊙O的半径和线段BE的长.
,CE=2.求⊙O的半径和线段BE的长.
查看答案和解析>>
科目:初中数学 来源:广东省汕头市澄海区2018届九年级上学期期末质量检测数学试卷 题型:解答题
解一元二次方程: 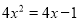 .
.
查看答案和解析>>
科目:初中数学 来源:广东省汕头市澄海区2018届九年级上学期期末质量检测数学试卷 题型:单选题
如图,四边形ABCD内接于⊙O,连接OB、OD,若∠BOD=∠BCD,则∠A的度数为( )
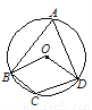
A. 60° B. 70° C. 120° D. 140°
A 【解析】试题解析:设 则 解得: 故选A.查看答案和解析>>
科目:初中数学 来源:2018人教版八年级数学下册练习:第十八章达标检测卷 题型:解答题
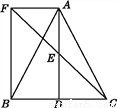
如图,△ABC中,D是BC边上的一点,E为AD的中点,过A作BC的平行线交CE的延长线于F,且AF=BD,连接BF.
(1)求证:BD=CD;
(2)如果AB=AC,试判断四边形AFBD的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源:2018人教版八年级数学下册练习:第十八章达标检测卷 题型:单选题
如图所示,平行四边形ABCD中,∠C=108°,BE平分∠ABC,则∠AEB等于( )
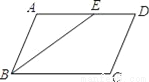
A. 180° B. 36° C. 72° D. 108°
B 【解析】【解析】 ∵AB∥CD, ∴∠ABC+∠C=180°, 把∠C=108°代入,得∠ABC=180°-108°=72°, 又∵BE平分∠ABC, ∴∠ABE=∠ABC=72°=36°, 故选B.查看答案和解析>>
科目:初中数学 来源:广东省东莞市翰林学校2017-2018学年八年级(上)期中数学试卷(word版含答案解析) 题型:单选题
如图所示的一块地,已知∠ADC=90°,AD=12m,CD=9m,AB=25m,BC=20m,则这块地的面积为( )平方米.
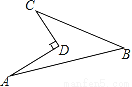
A. 96 B. 204 C. 196 D. 304
A 【解析】连接AC,运用勾股定理逆定理可证△ACD,△ABC为直角三角形,可求出两直角三角形的面积,此块地的面积为两个直角三角形的面积差. 【解析】 连接AC, 则在Rt△ADC中, AC2=CD2+AD2=122+92=225, ∴AC=15,在△ABC中,AB2=1521, AC2+BC2=152+362=1521, ∴AB2=AC2+BC2, ∴∠ACB=90...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com