已知二次函数y=2x2-mx-m2.
(1)求证:对于任意实数m,该二次函数图象与x轴总有公共点;
(2)若该二次函数图象与x轴有两个公共点A,B,且A点坐标为(1,0),求B点坐标.
【答案】
分析:(1)依题意可得△=9m
2得出△≥0,可得出二次函数图象与x轴总有公共点;
(2)把已知坐标代入可得m值,然后把m的值及y=0代入二次函数可求出点B的坐标.
解答:解:(1)当二次函数图象与x轴相交时,
2x
2-mx-m
2=0,
△=(-m)
2-4×2×(-m)
2=9m
2,
∵m
2≥0,
∴△≥0.
∴对于任意实数m,该二次函数图象与x轴总有公共点;
(2)把(1,0)代入二次函数关系式,得0=2-m-m
2,
∴m
1=-2,m
2=1,
当m=-2时,二次函数关系式为:y=2x
2+2x-4,
令y=0,得:2x
2+2x-4=0,
解得:x=1或-2,
∴二次函数图象与x轴有两个公共点的坐标是:(1,0),(-2,0);
又∵A点坐标为(1,0),则B(-2,0);
当m=1时,同理可得:B(
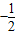
,0).
点评:利用二次函数与x轴的交点特征,转化为求△=b
2-4ac进行解答即可.

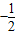 ,0).
,0).

 阅读快车系列答案
阅读快车系列答案