练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图,一块直角三角板的直角顶点P放在矩形ABCD的BC边上,并且使一条直角边经过点D,另一条直角边与AB交于点Q.

    （1）请你写出一对相似三角形,并加以证明;

    （2）若AB=6,BC=8,当PD=3PQ时,求PC的长.

    【答案】（1），证明见解析；（2）PC=6.

    【解析】

    （1）根据正方形推出∠B=∠C=∠QPD=90°，求出∠DPC=∠PQB，证△BPQ和△CDP相似即可；

    （2）根据相似得到比例式，把PD=3PQ代入求出即可．

    （1）△BPQ∽△CDP．证明如下：

    ∵正方形ABCD，∴∠B=∠C=90°．

    ∵∠QPD=90°，∴∠QPB+∠BQP=90°，∠QPB+∠DPC=90°，∴∠DPC=∠PQB，∴△BPQ∽△CDP．

    （2）设PC=x，则BP=8-x．

    ∵△BPQ∽△CDP，∴，即，解得：x=6．即PC=6．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】在研究相似问题时，甲、乙同学的观点如下：

    甲：将边长为3、4、5的三角形按图1的方式向外扩张，得到新三角形，它们的对应边间距为1，则新三角形与原三角形相似．

    乙：将邻边为3和5的矩形按图2的方式向外扩张，得到新的矩形，它们的对应边间距均为1，则新矩形与原矩形相似．

    对于两人的观点，下列说法正确的是（ ）

    A．甲对，乙不对 B．甲不对，乙对 C．两人都对 D．两人都不对

    查看答案和解析>>

    科目：初中数学 来源： 题型：

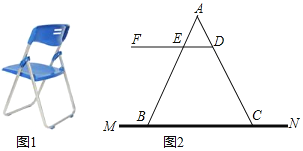
    【题目】如图1是一种折叠椅，忽略其支架等的宽度，得到他的侧面简化结构图图，支架与坐板均用线段表示，若座板DF平行于地面MN，前支撑架AB与后支撑架AC分别与座板DF交于点E、D，现测得厘米， 厘米， ．

    求椅子的高度即椅子的座板DF与地面MN之间的距离精确到1厘米

    求椅子两脚B、C之间的距离精确到1厘米参考数据：

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为响应荆州市“创建全国文明城市”号召，某单位不断美化环境，拟在一块矩形空地上修建绿色植物园，其中一边靠墙，可利用的墙长不超过18m，另外三边由36m长的栅栏围成．设矩形ABCD空地中，垂直于墙的边AB=xm，面积为ym2（如图）．

    （1）求y与x之间的函数关系式，并写出自变量x的取值范围；

    （2）若矩形空地的面积为160m2，求x的值；

    （3）若该单位用8600元购买了甲、乙、丙三种绿色植物共400棵（每种植物的单价和每棵栽种的合理用地面积如下表）．问丙种植物最多可以购买多少棵？此时，这批植物可以全部栽种到这块空地上吗？请说明理由．

    甲

    乙

    丙

    单价（元/棵）

    14

    16

    28

    合理用地（m2/棵）

    0.4

    1

    0.4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，矩形OABC的顶点O与平面直角坐标系的原点重合，点A，C分别在x轴，y轴上，点B的坐标为(－5，4)，点D为边BC上一点，连接OD，若线段OD绕点D顺时针旋转90°后，点O恰好落在AB边上的点E处，则点E的坐标为（ ）

    A. (－5，3） B. (－5，4) C. (－5，） D. (－5，2)

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读材料：以下是我们教科书中的一段内容，请仔细阅读，并解答有关问题．

    公元前3世纪，古希腊学家阿基米德发现：若杠杆上的两物体与支点的距离与其重量成反比，则杠杆平衡，后来人们把它归纳为“杠杆原理”，通俗地说，杠杆原理为：

    阻力×阻力臂=动力×动力臂

    （问题解决）

    若工人师傅欲用撬棍动一块大石头，已知阻力和阻力臂不变，分别为1500N和0.4m．

    （1）动力F（N）与动力臂l（m）有怎样的函数关系？当动力臂为1.5m时，撬动石头需要多大的力？

    （2）若想使动力F（N）不超过题（1）中所用力的一半，则动力臂至少要加长多少？

    （数学思考）

    （3）请用数学知识解释：我们使用棍，当阻力与阻力臂一定时，为什么动力臂越长越省力．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

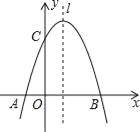
    【题目】如图，已知抛物线y=+mx+3与x轴交于A，B两点，与y轴交于点C，点B的坐标为（3，0），

    （1）求m的值及抛物线的顶点坐标．

    （2）点P是抛物线对称轴l上的一个动点，当PA+PC的值最小时，求点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知在关于x的分式方程 ①和一元二次方程（2﹣k）x2+3mx+（3﹣k）n=0②中，k、m、n均为实数，方程①的根为非负数．

    （1）求k的取值范围；

    （2）当方程②有两个整数根x1、x2，k为整数，且k=m+2，n=1时，求方程②的整数根；

    （3）当方程②有两个实数根x1、x2，满足x1（x1﹣k）+x2（x2﹣k）=（x1﹣k）（x2﹣k），且k为负整数时，试判断|m|≤2是否成立？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

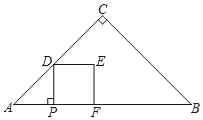
    【题目】如图，在△ABC中，∠C＝90°，AC＝BC，AB＝8．点P从点A出发，以每秒2个单位长度的速度沿边AB向点B运动．过点P作PD⊥AB交折线AC﹣CB于点D，以PD为边在PD右侧做正方形PDEF．设正方形PDEF与△ABC重叠部分图形的面积为S，点P的运动时间为t秒（0＜t＜4）．

    （1）当点D在边AC上时，正方形PDEF的边长为　 　（用含t的代数式表示）．

    （2）当点E落在边BC上时，求t的值．

    （3）当点D在边AC上时，求S与t之间的函数关系式．

    （4）作射线PE交边BC于点G，连结DF．当DF＝4EG时，直接写出t的值．

    查看答案和解析>>

    同步练习册答案