
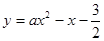 与x轴正半轴交于点A(3,0).以OA为边在x轴上方作正方形OABC,延长CB交抛物线于点D,再以BD为边向上作正方形BDEF.
与x轴正半轴交于点A(3,0).以OA为边在x轴上方作正方形OABC,延长CB交抛物线于点D,再以BD为边向上作正方形BDEF.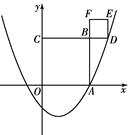
 中,得a=
中,得a= .
.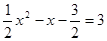 ,即x2-2x-9=0.
,即x2-2x-9=0.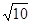 ,x2=1-
,x2=1-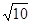 <0(舍去).
<0(舍去). 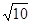 .
.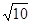 ,
,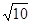 ).
). 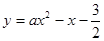 即可
即可

 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源:不详 题型:解答题
 ,
, ),且点B关于原点的对称点C也在该抛物线上.
),且点B关于原点的对称点C也在该抛物线上. 的点共有 个;
的点共有 个;查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 (单位:分钟)与学习收益量
(单位:分钟)与学习收益量 的关系如图1所示,用于回顾反思的时间
的关系如图1所示,用于回顾反思的时间 (单位:分钟)与学习收益
(单位:分钟)与学习收益 的关系如图2所示(其中
的关系如图2所示(其中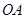 是抛物线的一部分,
是抛物线的一部分, 为抛物线的顶点),且用于回顾反思的时间不超过用于解题的时间.
为抛物线的顶点),且用于回顾反思的时间不超过用于解题的时间. 与用于解题的时间
与用于解题的时间 之间的函数关系式;
之间的函数关系式; 与用于回顾反思的时间
与用于回顾反思的时间 的函数关系式;
的函数关系式;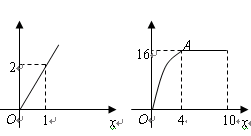
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 ,对角线AC与BD相交于O,AB=8cm,AD=10cm,BC=6cm,一个动点E从点B出发,以每秒1cm的速度沿射线BA方向移动,过E作EQ⊥AB,交直线AC于P,交直线BD于Q,以PQ为边向上作正方形PQMN,设正方形PQMN与△BOC,重叠部分的面积为s,点E的运动时间为t秒.
,对角线AC与BD相交于O,AB=8cm,AD=10cm,BC=6cm,一个动点E从点B出发,以每秒1cm的速度沿射线BA方向移动,过E作EQ⊥AB,交直线AC于P,交直线BD于Q,以PQ为边向上作正方形PQMN,设正方形PQMN与△BOC,重叠部分的面积为s,点E的运动时间为t秒.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

 (m),面积为
(m),面积为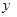 (m2),求
(m2),求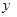 关于
关于 的函数关系式,并写出自变量
的函数关系式,并写出自变量 的取值范围;
的取值范围; 为何值时,所围苗圃的面积最大,最大面积是多少?
为何值时,所围苗圃的面积最大,最大面积是多少?查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
 的图象如图所示,给出下列说法:
的图象如图所示,给出下列说法:
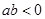 ;②方程
;②方程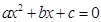 的根为
的根为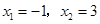 ;
; ;④当
;④当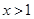 时,y随x值的增大而增大;
时,y随x值的增大而增大; 时,
时,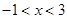 .
.查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| 1 |
| 4 |
| A.1 | B.2 | C.3 | D.4 |
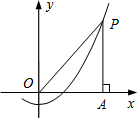
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com