
【题目】如图(1),OP是∠MON的平分线,请你利用该图形画一对以OP所在直线为对称轴的全等三角形.请你参考这个作全等三角形的方法,解答下列问题:
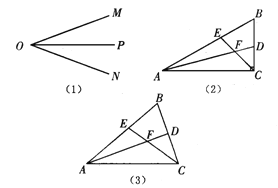
(1)如图(2),在△ABC中,∠ACB是直角,∠B=60°, AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F.请你判断并写出FE与FD之间的数量关系;
(2)如图(3),在△ABC中,如果∠ACB不是直角,而(1)中的其他条件不变,在(1)中所得结论是否仍然成立?请说明理由.
【答案】详见解析.
【解析】
试题分析:(1)在AC上截取AG=AE,连接FG.先证明△EAF≌△GAF,再证明△FDC≌△FGC,即可得结论;(2)根据(1)的方法证明即可.
试题解析:
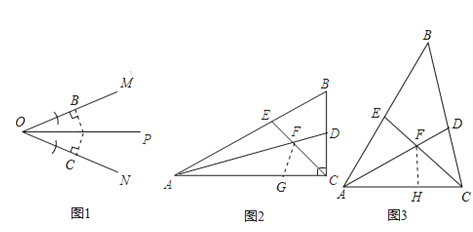
作对称全等三角形如图1.
(1)FE=FD.
如图2,∵∠ACB=90°,∠B=60°.
∴∠BAC=30°.
∵AD、CE分别是∠BAC和∠BCA的平分线,
∴∠EAF=∠CAF=![]() ∠BAC=15°,∠DCF=∠ACF=
∠BAC=15°,∠DCF=∠ACF=![]() ∠ACB=45°.
∠ACB=45°.
∴∠AEF=∠B+∠DCF=60°+45°=105°,
∴∠EFA=180°﹣∠AEF﹣∠EAF=60°.
如图2,在AC上截取AG=AE,连接FG.
∵∠EAF=∠GAF,
又∵AF为公共边,
∴△EAF≌△GAF,
∴FE=FG,∠EFA=∠GFA=60°.
∴∠GFC=180°﹣60°﹣60°=60°.
又∵∠DFC=∠EFA=60°,
∴∠DFC=∠GFC.
由(1)知∠DCF=∠GCF,
又∵CF为公共边,
∴△FDC≌△FGC,
∴FD=FG.
∴FE=FD.
(2)(1)中的结论FE=FD仍然成立.
同(2)可得△EAF≌△HAF,
∴FE=FH,∠EFA=∠HFA.
又由(1)知∠FAC=![]() ∠BAC,∠FCA=
∠BAC,∠FCA=![]() ∠ACB,
∠ACB,
∴∠FAC+∠FCA=![]() (∠BAC+∠ACB)=
(∠BAC+∠ACB)=![]() (180°﹣∠B)=60°.
(180°﹣∠B)=60°.
∴∠AFC=180°﹣(∠FAC+∠FCA)=120°.
∴∠EFA=∠HFA=180°﹣120°=60°.
同(2)可得△FDC≌△FHC,
∴FD=FH.
∴FE=FD.


科目:初中数学 来源: 题型:
【题目】如图,已知A(1,2),B(3,1),C(4,3).
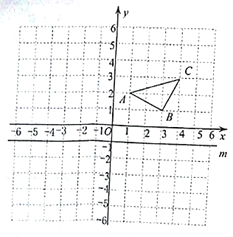
(1)作△ABC关于y轴的对称图形△A1B1C1,写出点C关于y轴的对称点C1的坐标;
(2)作△ABC关于直线m(直线m上各点的纵坐标都为-1)的对称图形△A2B2C2,写出点C关于直线m的对称点C2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:
为了提高产品的附加值,某公司计划将研发生产的1200件新产品进行精加工后再投放市场.现有甲、乙两个工厂都具备加工能力,公司派出相关人员分别到这两个工厂了解情况,获得如下信息:
信息一:甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多用10天;
信息二:乙工厂每天加工的数量是甲工厂每天加工数量的1.5倍.
根据以上信息,求甲、乙两个工厂每天分别能加工多少件新产品.
查看答案和解析>>
科目:初中数学 来源: 题型:
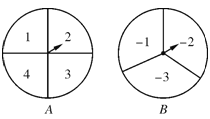
【题目】如图,甲、乙两人在玩转盘游戏时,准备了两个可以自由转动的转盘A、B,每个转盘被分成面积相等的几个扇形,并在每一个扇形内标上数字.游戏规则:同时转动两个转盘,当转盘停止后,指针所指区域的数字之和为0时,甲获胜;数字之和为1时,乙获胜.如果指针恰好指在分割线上,那么重转一次,直到指针指向某一区域为止.
(1)用画树状图或列表法求乙获胜的概率;
(2)这个游戏规则对甲、乙双方公平吗?请判断并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中有一点A,作点A关于y轴的对称点A′,再将点A′向下平移4个单位,得到点A′′(1,1),则点A的坐标是_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com