
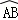 所在圆的圆心为O′时,求O′A的长度;
所在圆的圆心为O′时,求O′A的长度;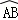 经过圆心为O时,求
经过圆心为O时,求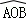 的长度;
的长度;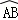 与
与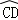 所在圆外切于点P时,设点O到弦AB.CD的距离之和为d,求d的值;
所在圆外切于点P时,设点O到弦AB.CD的距离之和为d,求d的值;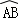 与
与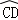 所在圆外切于点P时,设点M为AB的中点,点N为CD的中点,试探究四边形OMPN的形状,并证明你的结论.
所在圆外切于点P时,设点M为AB的中点,点N为CD的中点,试探究四边形OMPN的形状,并证明你的结论.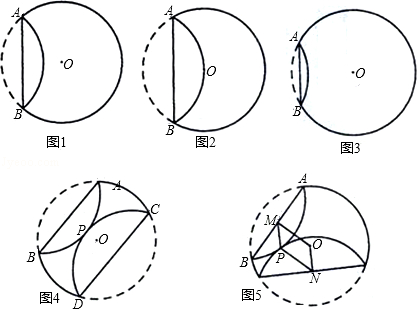
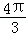 ,③
,③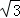 (2)①2,②平行四边形,证明见解析
(2)①2,②平行四边形,证明见解析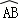 所在圆O′与⊙O是等圆,
所在圆O′与⊙O是等圆,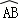 经过圆O时,折叠后的
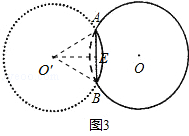
经过圆O时,折叠后的 所在圆O′在⊙O上,如图2所示,连接O′A.OA.O′B,OB,OO′
所在圆O′在⊙O上,如图2所示,连接O′A.OA.O′B,OB,OO′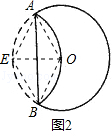
 =
=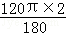 =
=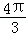 ;
;
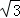 .
.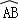 与
与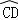 所在圆外切于点P时,
所在圆外切于点P时, 于点E,交CD于点G、交
于点E,交CD于点G、交 于点F,
于点F,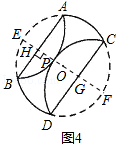
 PE,PG=
PE,PG= PF,
PF, PE+
PE+ PF=
PF= (PE+PF)=2,
(PE+PF)=2, 与
与 所在圆外切,
所在圆外切,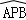 与
与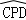 所在圆与⊙O是等圆,
所在圆与⊙O是等圆, OO″=ON,PM=ON,
OO″=ON,PM=ON,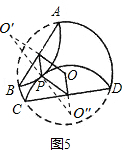
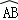 所在圆O′与⊙O是等圆,可得O′A的长度;
所在圆O′与⊙O是等圆,可得O′A的长度;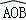 的圆心角,再根据弧长公式计算即可;
的圆心角,再根据弧长公式计算即可;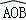 所在圆的圆心O′到弦AB的距离;
所在圆的圆心O′到弦AB的距离;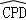 与
与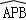 所在圆外切于点P时,过点O作EF⊥AB交
所在圆外切于点P时,过点O作EF⊥AB交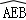 于于点E,交
于于点E,交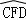 于点F,根据垂径定理及折叠,可求点O到AB.CD的距离之和;
于点F,根据垂径定理及折叠,可求点O到AB.CD的距离之和;

科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
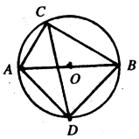
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
 ,大圆的弦
,大圆的弦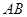 切小圆于
切小圆于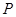 ,两圆的半径分别为
,两圆的半径分别为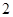 和
和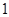 ,则弦长
,则弦长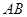 = ;若用阴影部分围成一个圆锥,则该圆锥的底面半径为 .(结果保留根号)
= ;若用阴影部分围成一个圆锥,则该圆锥的底面半径为 .(结果保留根号)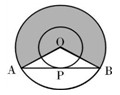
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com