
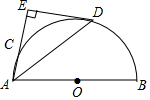
 如图,AB是半圆O的直径,且AB=4,点C是半圆上一点,半圆的切线DE垂直直线AC于点E.
如图,AB是半圆O的直径,且AB=4,点C是半圆上一点,半圆的切线DE垂直直线AC于点E.分析 (1)先利用切线的性质得OD⊥DE,则可判断OD∥AE,所以∠1=∠3,加上∠1=∠2,所以∠2=∠3;
(2)①连接CD、BD,如图,利用圆周角定理得到∠ADB=90°,则可证明△AED∽△ADB,利用相似比得到AD2=4AE,则DE2=$\frac{1}{4}$AE,再根据勾股定理得到$\frac{1}{4}$AE+AE2=4AE,解得AE=$\frac{15}{4}$;
②利用菱形的判定方法,当AC=AO=2时,四边形AODC为菱形,则△AOC和△OCD都是等边三角形,所以CD=2,∠ODC=60°,然后在Rt△CDE中利用含30度的直角三角形三边的关系得到CE=$\frac{1}{2}$CD=1,所以AE=3.
解答 (1)证明:∵DE为切线,
∴OD⊥DE,
∵AE⊥DE,
∴OD∥AE,
∴∠1=∠3,
∵OA=OD,
∴∠1=∠2,
∴∠2=∠3,
∴AD平分∠CAB;
(2)解:①连接CD、BD,如图,
∵AB是半圆O的直径,
∴∠ADB=90°,
∵∠2=∠3,
∴△AED∽△ADB,
∴AE:AD=AD:AB,
∴AD2=4AE,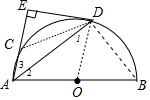
而AD=4DE,
∴DE2=$\frac{1}{4}$AE,
在Rt△ADE中,∵DE2+AE2=AD2,
∴$\frac{1}{4}$AE+AE2=4AE,解得AE=$\frac{15}{4}$,
即当AE=$\frac{15}{4}$时,AD=4DE;
②∵OA∥AC,OA=OD,
∴当AC=AO=2时,四边形AODC为菱形,
∴△AOC和△OCD都是等边三角形,
∴CD=2,∠ODC=60°,
在Rt△CDE中,∠CDE=30°,
∴CE=$\frac{1}{2}$CD=1,
∴AE=AC+CE=3,
即当AE=3时,四边形AODC是菱形.
故答案为$\frac{15}{4}$,3.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.也考查了圆周角定理、相似三角形的判定与性质和菱形的判定.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=-(x-1)2-3 | B. | y=-(x+1)2-3 | C. | y=-(x-1)2+3 | D. | y=-(x+a)2+3 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
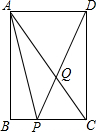 如图,矩形ABCD中,AB=4,AD=3,点Q在对角线AC上,且AQ=AD,连接DQ并延长,与边BC交于点P,则线段AP=$\sqrt{17}$.
如图,矩形ABCD中,AB=4,AD=3,点Q在对角线AC上,且AQ=AD,连接DQ并延长,与边BC交于点P,则线段AP=$\sqrt{17}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{21}$ | B. | $\sqrt{35}$ | C. | $\sqrt{42}$ | D. | $\root{3}{64}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
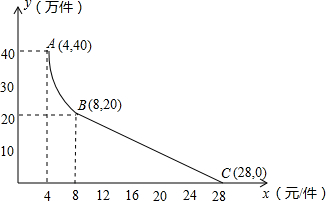 月电科技有限公司用160万元,作为新产品的研发费用,成功研制出了一种市场急需的电子产品,已于当年投入生产并进行销售.已知生产这种电子产品的成本为4元/件,在销售过程中发现:每年的年销售量y(万件)与销售价格x(元/件)的关系如图所示,其中AB为反比例函数图象的一部分,BC为一次函数图象的一部分.设公司销售这种电子产品的年利润为s(万元).(注:若上一年盈利,则盈利不计入下一年的年利润;若上一年亏损,则亏损计作下一年的成本.)
月电科技有限公司用160万元,作为新产品的研发费用,成功研制出了一种市场急需的电子产品,已于当年投入生产并进行销售.已知生产这种电子产品的成本为4元/件,在销售过程中发现:每年的年销售量y(万件)与销售价格x(元/件)的关系如图所示,其中AB为反比例函数图象的一部分,BC为一次函数图象的一部分.设公司销售这种电子产品的年利润为s(万元).(注:若上一年盈利,则盈利不计入下一年的年利润;若上一年亏损,则亏损计作下一年的成本.)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com