
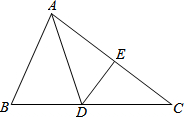
 如图,在△ABC中,DE⊥AC,垂足为E,∠EAD=∠ECD,AE=3cm,△ABD的周长为13cm,试找出图中相等的线段和相等的角并求出△ABC的周长.
如图,在△ABC中,DE⊥AC,垂足为E,∠EAD=∠ECD,AE=3cm,△ABD的周长为13cm,试找出图中相等的线段和相等的角并求出△ABC的周长. 分析 根据线段垂直平分线上的点到线段两端点的距离相等的性质可得AD=CD,然后求出△ABD的周长等于AB+BC,再求出AC的长,最后根据三角形的周长公式进行计算即可得解.
解答 解:图中相等的线段有:AD=CD,AE=CE,相等的角:∠ADE=∠CDE,∠AED=∠CED,
∵∠EAD=∠ECD,
∴AD=CD,
∵DE⊥AC,DE是AC的垂直平分线,AE=3cm,
∴AD=CD,AC=2AE=2×3=6cm,
∴△ABD的周长=AB+BD+AD=AB+BD+CD=AB+BC=13cm,
∴△ABC的周长=AB+BC+AC=13+6=19cm.
点评 本题主要考查了线段垂直平分线上的点到线段两端点的距离相等的性质,熟记性质是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 一正一负的两个有理数(零除外)称之为相反数 | |
| B. | 具有相反意义的两个数称之为相反数 | |
| C. | 在数轴上原点的两旁,离开原点距离相等的点所表示的两个数 | |
| D. | 符号不同的两个数 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
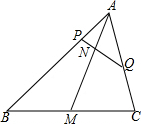 如图,已知△ABC,AM是中线,点P在边AB上,点Q在边AC上,PQ交AM于点N.
如图,已知△ABC,AM是中线,点P在边AB上,点Q在边AC上,PQ交AM于点N.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
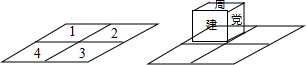 如图,平面上有四个方格,把一个正方体放在1号格上,向右翻转右侧面压在2号格上,再翻向3号格、4号格,再翻回1号格,这样循环翻动下去,如果开始时,正方体的正面、右侧面、后面、左侧面、顶面、底面依次写有“建党九十周年”字样,那么当正方体出发后周字第20次回到顶面时,正方体所在格是1号.
如图,平面上有四个方格,把一个正方体放在1号格上,向右翻转右侧面压在2号格上,再翻向3号格、4号格,再翻回1号格,这样循环翻动下去,如果开始时,正方体的正面、右侧面、后面、左侧面、顶面、底面依次写有“建党九十周年”字样,那么当正方体出发后周字第20次回到顶面时,正方体所在格是1号.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com