
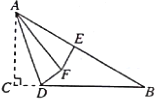
【题目】如图,已知在△ABC中,![]() ,
,![]() ,
,![]() ,点E为AB的中点,D为BC边上的一动点,把△ACD沿AD折叠,点C落在点F处,当△AEF为直角三角形时,CD的长为__________.
,点E为AB的中点,D为BC边上的一动点,把△ACD沿AD折叠,点C落在点F处,当△AEF为直角三角形时,CD的长为__________.
【答案】2或![]()
【解析】
本题以三角形为基础,考查内容包含中点的用法,可立刻推边等;动点图形翻折问题,可得到角等以及边等,解答本题需以题目要求直角三角形为前提,采取分类讨论方法,通过构造辅助线、假设未知数并结合勾股定理求解.
(1)当∠AFE=90°时
作EM⊥BC垂足为M.,作AN⊥ME于N,如下图所示:
∵∠C=∠EMB=90°
∴EM∥AC

∴∠C=∠CMN=∠N=90°
∴四边形ACMN是矩形
∵AC=CM=2
∴四边形ACMN是正方形
在RT△ABC中,∵AC=2,BC=4
∴AB=![]() ,AE=
,AE=![]()
在RT△AFE中,∵AE=![]() ,AF=AC=2
,AF=AC=2
∴FE=1
设CD=FD=x,在RT△EDM中,∵DE=1+x,EM=1,DM=2-x
∴![]()
![]()
![]()
∴CD=![]()

(2)当∠AFE=90°时,如下图所示
∵∠AFD=90°
∴F,E,D三点共线
在RT△AFE中,∵AE=![]() ,AF=AC=2
,AF=AC=2
∴EF=1
又∵DE=1
∴EF=ED
又∵EA=EB,∠AEF=∠BED
所以△AFE![]() △BDE(SAS)
△BDE(SAS)
∴∠BDE=∠AFE=90°
故四边形AFCD是矩形
又∵AF=AC
所以四边形AFCD是正方形
∴CD=AC=2



 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:初中数学 来源: 题型:
【题目】如图,将边长为10的正三角形OAB放置于平面直角坐标系xOy中,C是AB边上的动点(不与端点A,B重合),作CD⊥OB于点D,若点C,D都在双曲线y=![]() 上(k>0,x>0),则k的值为( )
上(k>0,x>0),则k的值为( )
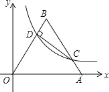
A. 25![]() B. 18
B. 18![]() C. 9D. 9
C. 9D. 9![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 交
交![]() 轴于
轴于![]() 两点,交
两点,交![]() 轴于点
轴于点![]() ,点
,点![]() 为线段
为线段![]() 下方抛物线上一动点,连接
下方抛物线上一动点,连接![]() .
.
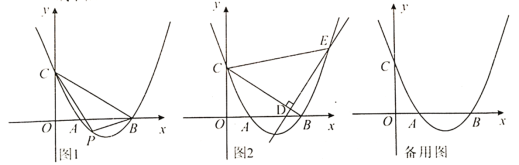
(1)求抛物线解析式;
(2)在点![]() 移动过程中,
移动过程中,![]() 的面积是否存在最大值?若存在,求出最大面积及点
的面积是否存在最大值?若存在,求出最大面积及点![]() 的坐标,若不存在,请说明理由;
的坐标,若不存在,请说明理由;
(3)设点![]() 为
为![]() 上不与端点重合的一动点,过点
上不与端点重合的一动点,过点![]() 作线段
作线段![]() 的垂线,交抛物线于点
的垂线,交抛物线于点![]() ,若
,若![]() 与
与![]() 相似,请直接写出点
相似,请直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
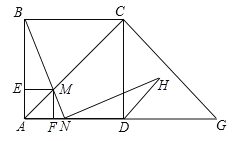
【题目】如图,在边长为2的正方形ABCD中,G是AD延长线上的一点,且DG=AD,动点M从A点出发,以每秒1个单位的速度沿着A→C→G的路线向G点匀速运动(M不与A,G重合),设运动时间为t秒,连接BM并延长交AG于N.
(1)当AM=_____________时,△ABM是以AB为底边的等腰三角形;
(2)当点N在AD边上时,若BN⊥HN,NH交∠CDG的平分线于H,求证:BN=HN;
(3)过点M分别作AB,AD的垂线,垂足分别为E,F,矩形AEMF与△ACG重叠部分的面积为S,求S与t的函数关系式,并求S最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,AC=BC,CD是⊙O的直径,与AB相交于点G,过点D作EF∥AB,分别交CA、CB的延长线于点E、F,连接BD.
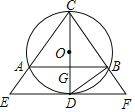
(1)求证:EF是⊙O的切线;
(2)求证:BD2=ACBF.
查看答案和解析>>
科目:初中数学 来源: 题型:
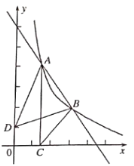
【题目】如图,点![]() 、
、![]() 是直线
是直线![]() 与反比例函数
与反比例函数![]() 图象的两个交点,
图象的两个交点,![]() 轴于点C,己知点D(0,1),连接AD、BD、BC,
轴于点C,己知点D(0,1),连接AD、BD、BC,
(1)求反比例函数和直线AB的表达式;
(2)根据函数图象直接写出当![]() 时不等式
时不等式![]() 的解集;
的解集;
(3)设△ABC和△ABD的面积分别为![]() 、
、![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() 的图象交于点A(﹣3,m+8),B(n,﹣6)两点.
的图象交于点A(﹣3,m+8),B(n,﹣6)两点.
(1)求一次函数与反比例函数的解析式;
(2)求△AOB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年12月16日扬州首批为民服务5G站点正式上线,自此有了5G网络.5G网络峰值速率为4G网络峰值速率的10倍,在峰值速率下传输500兆数据,5G网络比4G网络快45秒,求这两种网络的峰值速率.
查看答案和解析>>
科目:初中数学 来源: 题型:
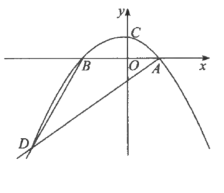
【题目】如图,在平面直角坐标系中,抛物线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() ,且经过点
,且经过点![]() ,连接
,连接![]() .
.
(1)求该抛物线的函数关系式;
(2)△ANM与![]() 是否相似?若相似,请求出此时点
是否相似?若相似,请求出此时点![]() 、点
、点![]() 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;
(3)若点![]() 是直线
是直线![]() 上方的抛物线上一动点(不与点
上方的抛物线上一动点(不与点![]() 重合),过
重合),过![]() 作
作![]() 轴交直线
轴交直线![]() 于点
于点![]() ,以
,以![]() 为直径作⊙
为直径作⊙![]() ,则⊙
,则⊙![]() 在直线
在直线![]() 上所截得的线段长度的最大值等于 .(直接写出答案)
上所截得的线段长度的最大值等于 .(直接写出答案)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com