
【题目】在矩形纸片ABCD中,AD=8,AB=6,E是边BC上的点,将纸片沿AE折叠,使点B落在点F处,连接FC,当△EFC为直角三角形时,BE的长为( )
A. 3 B. 5 C. 3或5 D. 3或6
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,数轴上有三个点A、B、C,表示的数分别是-4、-2、3,请回答:
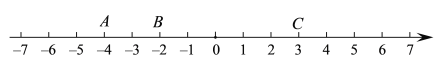
(1)若C、B两点的距离与A、B两点距离相等,则需将点C向左移动________个单位;
(2)若移动A、B、C三点中的两点,使三个点表示的数相同,移动方法有________种,其中移动所走的距离之和最小的是________个单位;
(3)若在B处有一小青蛙,一步跳一个单位长,小青蛙第一次先向左跳一步,第2次向右跳3步,第3次向再向左跳5步,第4次再向右跳7步……,按此规律继续下去,那么跳第100次时落脚点表示的数是________;
(4)若有两只小青蛙M、N,它们在数轴上的点表示的数分别为整数x、y,且|x-2|+|y+3|=2,求两只青蛙M、N之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
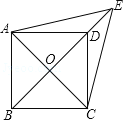
【题目】如图,已知平行四边形ABCD中,对角线AC,BD交于点O,E是BD延长线上的点,且△ACE是等边三角形.
(1)求证:四边形ABCD是菱形;
(2)若∠AED=2∠EAD,求证:四边形ABCD是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一条笔直公路BD的正上方A处有一探测仪,AD=24m,∠D=90°,一辆轿车从B点匀速向D点行驶,测得∠ABD=31°,2秒后到达C点,测得∠ACD=50°.
(Ⅰ)求B,C两点间的距离(结果精确到1m);
(Ⅱ)若规定该路段的速度不得超过15m/s,判断此轿车是否超速.
参考数据:tan31°≈0.6,tan50°≈1.2.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,![]() 的顶点均在格点上,点
的顶点均在格点上,点![]() 的坐标为
的坐标为![]() .
.

①把![]() 向上平移5个单位后得到对应的
向上平移5个单位后得到对应的![]() ,画出
,画出![]() ,并写出
,并写出![]() 的坐标;
的坐标;
②以原点![]() 为对称中心,画出
为对称中心,画出![]() 与关于原点
与关于原点![]() 对称的
对称的![]() ,并写出点
,并写出点![]() 的坐标.
的坐标.
③以原点O为旋转中心,画出把![]() 顺时针旋转90°的图形△A3B3C3,并写出C3的坐标.
顺时针旋转90°的图形△A3B3C3,并写出C3的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某巡警骑摩托车在一条东西直大道上巡逻,某天他从岗亭出发,晚上停留在A处,规定向东方向为正,当天行驶情况记录如下(单位:千米):
+9, -5, +7, -14, +1, -10, +8;
(1)点A在岗亭的 边方向,距离岗亭 千米。
(2)若他离开岗亭超过10千米对讲机就会与岗亭值班员失联,请问他这一天有没有失联过?有几次?请说明理由。
(3)若摩托车每行驶100千米耗油6升,这一天共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过正方形ABCD的顶点D作DE∥AC交BC的延长线于点E.
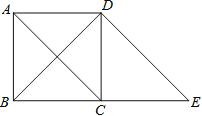
(1)判断四边形ACED的形状,并说明理由;
(2)若BD=8cm,求线段BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市居民阶梯水价按照月用水量为单位实施,当累计水量达到月阶梯水量分档基数临界点后,即开始实施阶梯加价,分档水量和价格具体如下:
第一阶梯:户月用水量为0-18吨(含)部分,每吨自来水价格为a元;
第二阶梯:户月用水量为18-25吨(含)部分,每吨自来水价格为b元;
第三阶梯:户月用水量为25吨以上的部分,每吨自来水价格为5元.
(1)已知小蔡家10月用水15吨,水费30元;11月份用水23吨,水费51元,则a= ,b= .
(2)12月份,小张拜托小蔡帮忙缴纳水费,12月份小蔡家和小张家共缴纳水费111元,已知小蔡家和小张家12月份水量都是整数,且小蔡家本月用水量超过了18吨,则12月份两家各自用水量可能是多少吨?
(3)某月小蔡家比小王家多交水费28元,小王家比小张家多交水费17元,则三户共交水费多少元?(三户用水量都是整数)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com