
”¾ĢāÄæ”æijµēŹÓĢØĪŖĮĖ½ā±¾µŲĒųµēŹÓ½ŚÄæµÄŹÕŹÓĒéæö£¬¶Ō²æ·Ö¹ćÖŻæŖÕ¹ĮĖ”°Äć×īĻ²°®µÄµēŹÓ½ŚÄæ”±µÄĪŹ¾ķµ÷²é£ØĆæČĖÖ»ĢīŠ“Ņ»Ļī£©£¬øł¾ŻŹÕ¼ÆµÄŹż¾Ż»ęÖĘĮĖĻĀĆęĮ½·ł²»ĶźÕūµÄĶ³¼ĘĶ¼£¬øł¾ŻŅŖĒó»Ų“šĻĀĮŠĪŹĢā£ŗ
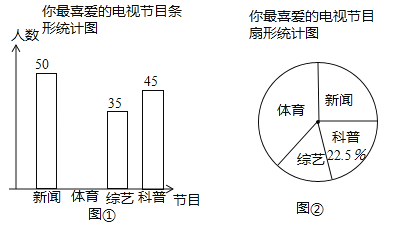
£Ø1£©±¾“ĪĪŹ¾ķµ÷²é¹²µ÷²éĮĖ Ćū¹ŪÖŚ£»
£Ø2£©Ķ¼¢ŚÖŠ×īĻ²°®”°ŠĀĪŽŚÄæ”±µÄČĖŹżÕ¼µ÷²é×ÜČĖŹżµÄ°Ł·Ö±ČĪŖ £¬”°×ŪŅÕ½ŚÄæ”±ŌŚÉČŠĪĶ³¼ĘĶ¼ÖŠĖł¶ŌÓ¦µÄŌ²ŠÄ½ĒµÄ¶ČŹżĪŖ £»
£Ø3£©²¹Č«Ķ¼¢ŁÖŠµÄĢõŠĪĶ³¼ĘĶ¼£»
£Ø4£©ĻÖÓŠ×īĻ²°®”°ŠĀĪŽŚÄæ”±£Ø¼ĒĪŖ![]() £©£¬”°ĢåÓż½ŚÄæ”±£Ø¼ĒĪŖ
£©£¬”°ĢåÓż½ŚÄæ”±£Ø¼ĒĪŖ![]() £©£¬”°×ŪŅÕ½ŚÄæ”±£Ø¼ĒĪŖC£©£¬”°æĘĘÕ½ŚÄæ”±£Ø¼ĒĪŖD£©µÄ¹ŪÖŚø÷Ņ»Ćū£¬µēŹÓĢØŅŖ“ÓĖÄČĖÖŠĖ껜³éČ”Į½ČĖ²Ī¼ÓĮŖŅź»ī¶Æ£¬ĒėÓĆĮŠ±ķ»ņ»Ź÷דĶ¼µÄ·½·Ø£¬Ēó³öĒ”ŗĆ³éµ½×īĻ²°®”°B”±ŗĶ”°C”±Į½Ī»¹ŪÖŚµÄøÅĀŹ£®
£©£¬”°×ŪŅÕ½ŚÄæ”±£Ø¼ĒĪŖC£©£¬”°æĘĘÕ½ŚÄæ”±£Ø¼ĒĪŖD£©µÄ¹ŪÖŚø÷Ņ»Ćū£¬µēŹÓĢØŅŖ“ÓĖÄČĖÖŠĖ껜³éČ”Į½ČĖ²Ī¼ÓĮŖŅź»ī¶Æ£¬ĒėÓĆĮŠ±ķ»ņ»Ź÷דĶ¼µÄ·½·Ø£¬Ēó³öĒ”ŗĆ³éµ½×īĻ²°®”°B”±ŗĶ”°C”±Į½Ī»¹ŪÖŚµÄøÅĀŹ£®
”¾“š°ø”æ£Ø1£©200£»£Ø2£©40%£¬63”ć£»£Ø3£©×÷Ķ¼¼ū½āĪö£»£Ø4£©![]() £®
£®
”¾½āĪö”æ
ŹŌĢā·ÖĪö£ŗ£Ø1£©ÓĆĻ²»¶æĘĘÕ½ŚÄæµÄČĖŹż³żŅŌĖüĖłÕ¼µÄ°Ł·Ö±Č¼“æɵƵ½µ÷²éµÄ×ÜČĖŹż£»
£Ø2£©ÓĆĻ²°®”°ŠĀĪŽŚÄæ”±µÄČĖŹż³żŅŌµ÷²é×ÜČĖŹżµĆµ½ĖüĖłÕ¼µÄ°Ł·Ö±Č£¬Č»ŗóÓĆ360¶Č³ĖŅŌĻ²»¶”°×ŪŅÕ½ŚÄæ”±µÄČĖŹżĖłÕ¼µÄ°Ł·Ö±ČµĆµ½×ŪŅÕ½ŚÄæ”±ŌŚÉČŠĪĶ³¼ĘĶ¼ÖŠĖł¶ŌÓ¦µÄŌ²ŠÄ½ĒµÄ¶ČŹż£»
£Ø3£©ÓƵ÷²éµÄ×ÜČĖŹż·Ö±š¼õČ„Ļ²»¶ŠĀĪÅ”¢×ŪŅÕ”¢æĘĘÕµÄČĖŹżµĆµ½Ļ²»¶ĢåÓżµÄČĖŹż£¬Č»ŗó²¹Č«Ķ¼¢ŁÖŠµÄĢõŠĪĶ³¼ĘĶ¼£»
£Ø4£©»Ź÷דĶ¼Õ¹Ź¾ĖłÓŠ12ÖÖµČæÉÄܵĽį¹ūŹż£¬ŌŁÕŅ³ö³éµ½×īĻ²°®”°B”±ŗĶ”°C”±Į½Ī»¹ŪÖŚµÄ½į¹ūŹż£¬Č»ŗóøł¾ŻøÅĀŹ¹«Ź½Ēó½ā£®
ŹŌĢā½āĪö£ŗ£Ø1£©±¾“ĪĪŹ¾ķµ÷²é¹²µ÷²éµÄ¹ŪÖŚŹżĪŖ45”Ā22.5%=200£ØČĖ£©£»
£Ø2£©Ķ¼¢ŚÖŠ×īĻ²°®”°ŠĀĪŽŚÄæ”±µÄČĖŹżÕ¼µ÷²é×ÜČĖŹżµÄ°Ł·Ö±ČĪŖ50”Ā200=40%£»”°×ŪŅÕ½ŚÄæ”±ŌŚÉČŠĪĶ³¼ĘĶ¼ÖŠĖł¶ŌÓ¦µÄŌ²ŠÄ½ĒµÄ¶ČŹżĪŖ360”ć”Į![]() =63”ć£»
=63”ć£»
¹Ź“š°øĪŖ£ŗ200£¬40%£¬63”ć£»
£Ø3£©×īĻ²°®”°ŠĀĪŽŚÄæ”±µÄČĖŹżĪŖ200©50©35©45=70£ØČĖ£©£¬ČēĶ¼£ŗ

£Ø4£©»Ź÷דĶ¼ĪŖ£ŗ

¹²ÓŠ12ÖÖµČæÉÄܵĽį¹ūŹż£¬Ē”ŗĆ³éµ½×īĻ²°®”°B”±ŗĶ”°C”±Į½Ī»¹ŪÖŚµÄ½į¹ūŹżĪŖ2£¬ĖłŅŌĒ”ŗĆ³éµ½×īĻ²°®”°B”±ŗĶ”°C”±Į½Ī»¹ŪÖŚµÄøÅĀŹ=![]() =
=![]() £®
£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijŠ£¾ÅÄź¼¶£Ø1£©°ąĖłÓŠŃ§Éś²Ī¼Ó2016Äź³õÖŠ±ĻŅµÉśÉżŃ§ĢåÓż²āŹŌ£¬øł¾Ż²āŹŌĘĄ·Ö±ź×¼£¬½«ĖūĆĒµÄ³É¼Ø½ųŠŠĶ³¼Ęŗó·ÖĪŖA”¢B”¢C”¢DĖÄµČ£¬²¢»ęÖĘ³ÉČēĶ¼ĖłŹ¾µÄĢõŠĪĶ³¼ĘĶ¼ŗĶÉČŠĪĶ³¼ĘĶ¼£ØĪ“Ķź³É£©£¬Ēė½įŗĻĶ¼ÖŠĖłøųŠÅĻ¢½ā“šĻĀĮŠĪŹĢā£ŗ
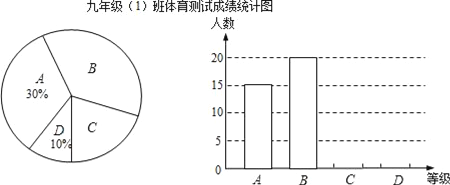
£Ø1£©¾ÅÄź¼¶£Ø1£©°ą²Ī¼ÓĢåÓż²āŹŌµÄѧɜӊ____ČĖ£»
£Ø2£©½«ĢõŠĪĶ³¼ĘĶ¼²¹³äĶźÕū£»
£Ø3£©ŌŚÉČŠĪĶ³¼ĘĶ¼ÖŠ£¬µČ¼¶B²æ·ÖĖłÕ¼µÄ°Ł·Ö±ČŹĒ____£¬µČ¼¶C¶ŌÓ¦µÄŌ²ŠÄ½ĒµÄ¶ČŹżĪŖ____£»
£Ø4£©ČōøĆŠ£¾ÅÄź¼¶Ń§Éś¹²ÓŠ850ČĖ²Ī¼ÓĢåÓż²āŹŌ£¬¹Ą¼Ę“ļµ½A¼¶ŗĶB¼¶µÄѧɜ¹²ÓŠ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æÖ»ĮŠ×ŪŗĻĖćŹ½»ņ·½³Ģ£¬²»¼ĘĖć
¢ŁÅ©»ś³§Éś²ś8700ĢØĶŃĮ£»ś£¬ŅŃ¾Éś²śĮĖ12Ģģ£¬ĆæĢģÉś²ś500ĢØ£¬Ź£ĻĀµÄ3ĢģĶź³É£¬Ę½¾łĆæĢģÉś²ś¶ąÉŁĢØ£æ
¢Ś³¬ŹŠ×¼±øŠŅŌĖĆž½±£¬»ī¶Æ×éŠčŅŖ×¼±øŅ»Š©ŗģĒņŗĶĀĢĒņ£¬ĻÖÓŠ15øöŗģĒņ£¬ŅŖČĆĆžµ½ŗģĒņµÄæÉÄÜŠŌŹĒ![]() £¬Ó¦øĆ×¼±ø¶ąÉŁøöĀĢĒņ? ______________________
£¬Ó¦øĆ×¼±ø¶ąÉŁøöĀĢĒņ? ______________________
¢ŪŠ”Ó¢°Ń1000ŌŖ°“ÄźĄūĀŹ3.15%“ęČėŅųŠŠ£¬Į½Äźŗó£¬ĖżæÉŅŌČ”»Ų¶ąÉŁĒ®£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚÕż±ČĄżŗÆŹży=ØC3mxÖŠ£¬ŗÆŹżyµÄÖµĖęxÖµµÄŌö“ó¶ųŌö“ó£¬ŌņP£Øm£¬5£©ŌŚ£Ø £©
A. µŚŅ»ĻóĻŽB. µŚ¶žĻóĻŽ
C. µŚČżĻóĻŽD. µŚĖÄĻóĻŽ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ¼ĘĖć£5+6£¬½į¹ūÕżČ·µÄŹĒ( ).
A. 1 B. £1 C. 11 D. £11
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĻĀĮŠ¼ĘĖćÕżČ·µÄŹĒ£Ø £©
A.£Øxy£©3=xy3
B.x5”Āx5=x
C.3x25x3=15x5
D.5x2y3+2x2y3=10x4y9
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ¼×”¢ŅŅĮ½ČĖ½ųŠŠÉä»÷²āŹŌ£¬ĆæČĖ20“ĪÉä»÷³É¼ØµÄĘ½¾łŹż¶¼ŹĒ8.5»·£¬·½²ī·Ö±šŹĒ£ŗS¼×2=3£¬SŅŅ2=2.5£¬ŌņÉä»÷³É¼Ø½ĻĪČ¶ØµÄŹĒ£ØĢī”°¼×”±»ņ”°ŅŅ”±£©£®
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com