
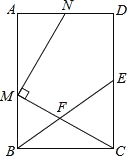
【题目】如图,在矩形ABCD中,E为CD的中点,F为BE上的一点,连结CF并延长交AB于点M,MN⊥CM交射线AD于点N.
(1)当F为BE中点时,求证:AM=CE;
(2)若![]() ,求
,求![]() 的值.
的值.
【答案】(1)证明见解析 (2)3
【解析】
(1)根据矩形的对边平行可得AB∥CD,再根据两直线平行,内错角相等求出∠BAC=∠FCO,然后利用“角角边”证明△AOE和△COF全等,再根据全等三角形的即可得证;
(2)连接OB,根据等腰三角形三线合一的性质可得BO⊥EF,再根据矩形的性质可得OA=OB,根据等边对等角的性质可得∠BAC=∠ABO,再根据三角形的内角和定理列式求出∠ABO=30°,即∠BAC=30°,根据直角三角形30°角所对的直角边等于斜边的一半求出AC,再利用勾股定理列式计算即可求出AB.
解:(1)当F为BE中点时,如图1,
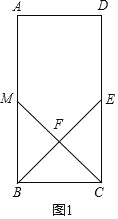
则有BF=EF.
∵四边形ABCD是矩形,
∴AB=DC,AB∥DC,
∴∠MBF=∠CEF,∠BMF=∠ECF.
在△BMF和△ECF中,
∵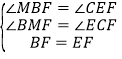 ,
,
∴△BMF≌△ECF,
∴BM=EC.
∵E为CD的中点,
∴EC=![]() DC,
DC,
∴BM=EC=![]() DC=
DC=![]() AB,
AB,
∴AM=BM=EC;
(2)如图2所示:设MB=a,
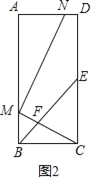
∵四边形ABCD是矩形,
∴AD=BC,AB=DC,∠A=∠ABC=∠BCD=90°,AB∥DC,
∴△ECF∽△BMF,
∴EC:BM=EF:BF=2,
∴EC=2a,
∴AB=CD=2CE=4a,AM=AB﹣MB=3a.
∵AB:BC=2,
∴BC=AD=2a.
∵MN⊥MC,
∴∠CMN=90°,
∴∠AMN+∠BMC=90°.
∵∠A=90°,
∴∠ANM+∠AMN=90°,
∴∠BMC=∠ANM,
∴△AMN∽△BCM,
∴AN:BM=AM:BC,
∴AN:a=3a:2a,
∴AN=![]() a,ND=AD﹣AN=2a﹣a=
a,ND=AD﹣AN=2a﹣a=![]() a,
a,
∴![]() =
=![]() =3.
=3.


科目:初中数学 来源: 题型:
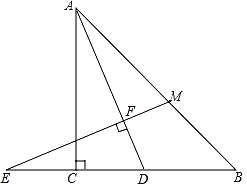
【题目】如图,在等腰Rt△ABC中,∠ACB=90°,AC=BC,D是线段BC上一动点(不与点B、C重合),连接AD,延长BC至点E,使得CE=CD,过点E作EF⊥AD于点F,再延长EF交AB于点M.
(1)若D为BC的中点,AB=4,求AD的长;
(2)求证:BM=![]() CD.
CD.
查看答案和解析>>
科目:初中数学 来源: 题型:
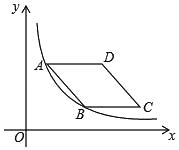
【题目】如图,菱形ABCD的边AD与x轴平行,A、B两点的横坐标分别为1和3,反比例函数y=![]() 的图象经过A、B两点,则菱形ABCD的面积是_____;
的图象经过A、B两点,则菱形ABCD的面积是_____;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,市防汛指挥部决定对某水库的水坝进行加高加固,设计师提供的方案是:水坝加高1米(EF=1米),背水坡AF的坡度i=1∶1,已知AB=3米,∠ABE=120°,求水坝原来的高度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,阳光下,小亮的身高如图中线段AB所示,他在地面上的影子如图中线段BC所示,线段DE表示旗杆的高,线段FG表示一堵高墙.
(1)请你在图中画出旗杆在同一时刻阳光照射下形成的影子,并用线段表示;
(2)如果小亮的身高AB=1.6m,他的影子BC=2.4m,旗杆的高DE=15m,旗杆与高墙的距离EG=16m,请求出旗杆的影子落在墙上的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】知识是用来为人类服务的,我们应该把它们用于有意义的方面.下面就两个情景请你作出评判.
情景一:从教室到图书馆,总有少数同学不走人行道而横穿草坪,这是为什么呢?试用所学数学知识来说明这个问题.

情景二:A、B是河流l两旁的两个村庄,现要在河边修一个抽水站向两村供水,问抽水站修在什么地方才能使所需的管道最短?请在图中表示出抽水站点P的位置,并说明你的理由:

你赞同以上哪种做法?你认为应用数学知识为人类服务时应注意什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
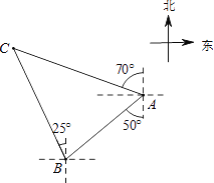
【题目】如图,国家规定休渔期间,我国渔政船在A处发现南偏西50°方向距A处20海里的点B处有一艘可疑船只,可疑船只正沿北偏西25°方向航行,我国渔政船立即沿北偏西70°方向前去拦截,经过1.5小时刚好在C处拦截住可疑船只,求该可疑船只航行的平均速度.
(结果精确到个位,参考数据: ![]() ≈1.4,
≈1.4, ![]() ≈1.7)
≈1.7)
查看答案和解析>>
科目:初中数学 来源: 题型:
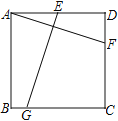
【题目】如图,在边长为6的正方形ABCD中,点F为CD上一点,E是AD的中点,且DF=2.在BC上找点G,使EG=AF,则BG的长是___________
查看答案和解析>>
科目:初中数学 来源: 题型:
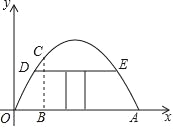
【题目】有一个抛物线型蔬菜大棚,将其截面放在如图所示的平面直角坐标系中,抛物线可以用函数y=ax2+bx来表示,已知OA=8米,距离O点2米处的棚高BC为![]() 米.
米.
(1)求该抛物线的解析式;
(2)若借助横梁DE(DE∥OA)建一个门,要求门的高度为1.5米,求横梁DE的长度是多少米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com