
设直线a∥b,在a上任取两点A,B,在直线b上任取两点C,D,再在两平行线之间任取一点E,试判断∠BED,∠ABE,∠EDC之间有何关系?请猜想并证明你的结论.
|
解:连接BD(如图)(1)当E点在线段BD上时,如图1,这时∠BED=
(2)当点E在线段BD的左侧时,如图2,过E点作EF∥AB,交BD于F,所以EF∥CD(平行公理的推论),所以∠BEF=∠ABE,∠FED=∠EDC(两直线平行,内错角相等),所以∠BEF+∠FED=∠ABE+∠EDC(等量性质),即∠BED=∠ABE+∠EDC
(3)当点E在线段BD的右侧时,如图3,过E点作EF∥AB交BD于F,所以EF∥CD,所以∠ABE+∠BEF=
综上所述可知:当E在BD上或BD的左侧时,∠BED=∠ABE+∠EDC;当E点在BD的右侧时,∠BED+∠ABE+∠EDC= 解题指导:连接线段BD,考虑到E点与BD之间的位置关系:点E可能在BD上,也可能在线段BD的左侧,还可能在线段BD的右侧,故解答此问题应注意分三种情况进行讨论 |


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
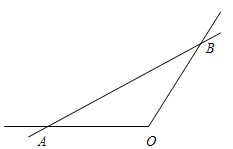 建一条高速公路L,新建高速公路在OA上设一出入口A,在OB上设一出入口B,高速公路在AB段为直线段.
建一条高速公路L,新建高速公路在OA上设一出入口A,在OB上设一出入口B,高速公路在AB段为直线段.查看答案和解析>>
科目:初中数学 来源: 题型:
 37、如图所示,过圆上两点AB作一直线,点M在圆上,点P在圆外,且点M,P在AB同侧,∠AMB=50°,设∠APB=x,当点P移动时,求x的变化范围,并说明理由,当点P移至圆内时,x有什么变化(直接写出结果)
37、如图所示,过圆上两点AB作一直线,点M在圆上,点P在圆外,且点M,P在AB同侧,∠AMB=50°,设∠APB=x,当点P移动时,求x的变化范围,并说明理由,当点P移至圆内时,x有什么变化(直接写出结果)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,过圆上两点AB作一直线,点M在圆上,点P在圆外,且点M,P在AB同侧,∠AMB=50°,设∠APB=x,当点P移动时,求x的变化范围,并说明理由,当点P移至圆内时,x有什么变化(直接写出结果)
如图所示,过圆上两点AB作一直线,点M在圆上,点P在圆外,且点M,P在AB同侧,∠AMB=50°,设∠APB=x,当点P移动时,求x的变化范围,并说明理由,当点P移至圆内时,x有什么变化(直接写出结果)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 建一条高速公路L,新建高速公路在OA上设一出入口A,在OB上设一出入口B,高速公路在AB段为直线段.
建一条高速公路L,新建高速公路在OA上设一出入口A,在OB上设一出入口B,高速公路在AB段为直线段.查看答案和解析>>
科目:初中数学 来源:2008-2009学年度第一学期九年级“五校”联考数学试卷(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com